第２５３問の解答

---

１．問題　［場合の数］

４ケタの整数の中で、１ケタ目と２ケタ目の数字の和と、３ケタ目と４ケタ目の数字の和が等しい数を考えます。 例えば、４５７２は、１ケタ目と２ケタ目の数字の和が４＋５＝９、３ケタ目と４ケタ目の数字の和が７＋２＝９で、等しくなっていますね。 では、このような整数は全部で何個あるでしょうか。

---

２．解答例１（ちえんかん＃２期さん、ＡЯＯＴさん、ミミズクはくず耳さん、高橋道広さん、あんみつさん、中村明海さん、BossFさん、M.Hossieさん、他多数）

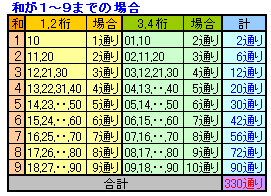
（和が１〜９までの場合）

１ケタ目は０にならないことに注意しながら数え上げると下表のように３３０通りとなります。

（和が１０〜１８までの場合）

１、２ケタ目と３、４ケタ目は同じなので、下表のように２８５通りとなります。

従って、合計３３０＋２８５＝６１５通りとなります。

　

答：６１５通り

以上

---

（参考）数列の和として求める方法

• 1、2、・・、n の和がS_n＝n(n+1)/2であることはよく知られています。
  実際、
  　S_n=1+　2+　・・+n　　・・・　（１）
  　S_n=n+(n-1)+・・+1　　・・・　（２）
  （１）＋（２）より、
  　２S_n=(n+1)+(n+1)+・・+(n+1)＝n(n+1)
  よって、S_n＝n(n+1)/2
  
  
• 1²、2²、・・、n² の和は、S_n＝n(n+1)(2n+1)/6が成り立ちます。
  k(k+1)(2k+1)-(k-1)k(2k-1)＝6k²より、
  　６Σ_(k=1..n)k²
  ＝Σ_(k=1..n)k(k+1)(2k+1)-Σ_(k=1..n)(k-1)k(2k-1)
  ＝n(n+1)(2n+1)-0・１・１
  よって、S_n＝n(n+1)(2n+1)/6

本題では、
　Σ_(k=1..9)k(k+1)＋Σ_(k=1..9)k²
＝(Σ_(k=1..9)k²＋Σ_(k=1..9)k）＋Σ_(k=1..9)k²
＝(9・10・19/6＋9・10/2)＋9・10・19/6
＝（285＋45)＋285
＝615通り　と求めることができます。

　

---