第254問の解答
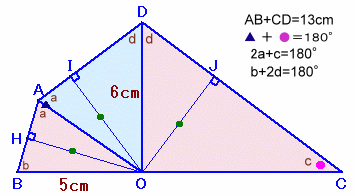
1.問題 [平面図形]
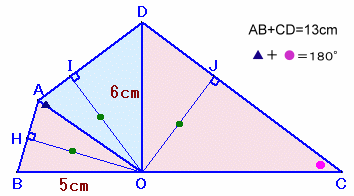 |
|
2.解答例1(ちーくん、高橋道広さん、吉川マサルさん、他)
△OAH≡△OAIより、∠OAH=∠OAI=aとおきます。
同様に、△ODI≡△ODJより、∠ODI=∠ODJ=dとおきます。
題意より、2a+c=180度。
四角形ABCDの内角の和は360度だから、b+2a+2d+c=360度、
よって、b+2d=180度と分かります。さて、点B'を辺AD上に、IB'=HBとなるようにとります。
(ちーくんの解法による)
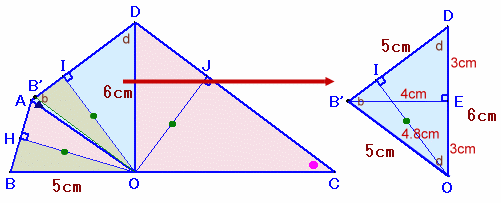
△B'DOについて、内角の和は180度だから、
∠DOB'+b+d=180
よって、∠DOB'=dとなり、△B'DOはB'D=B'Oの二等辺三角形となります。次に、B'からDOに下ろした垂線の足をEとすると、DE=OE=3cm。
従って、△DEB'≡△OEB'は、辺の長さが3:4:5の直角三角形と分かります。また、△DIO∽△DEB'より、OI=DB×B'E/BD=6×4/5=4.8cm。
よって、OH=OJ=OI=4.8cm。従って、
△ABO+△DOC
=1/2×AB×OH+1/2×CD×OJ
=1/2×(AB+CD)×4.8
=1/2×13×4.8
=31.2cm2なお、高橋道広さんは、点B'を辺CD上にOB=OB'となるように取り、
また、マサルさんは、△DIOを点Oを基点として回転してOIがOHに重なるようにして、
いずれも上記とほぼ同様に解いています。答:31.2cm2
以上
3.解答例2(武田浩紀さん、圭太さん、医学部性さん、水田江楠さん、小西孝一さん、他)
△ABOと△DOCを、ABとDCを底辺にしてくっつけます。
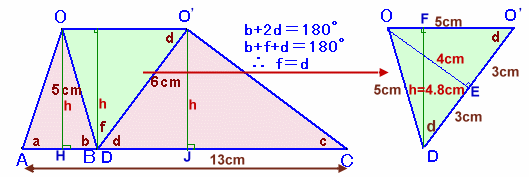
すると、OH=O'J(=hとおく)なので、OO'はACと平行になります。
△ODO'について、∠OBO'=fとおくと、b+f+d=180度になります。
ところが、解答例1で得たように、b+2d=180度なので、f=d、
よって、△ODO'は、OD=OO'の二等辺三角形となります。OからDO'に、およびDからOO'に下ろした垂線の足をそれぞれE、Fとします。
DE=O'E=3cmより、△OE'Oは、辺の長さが3:4:5の直角三角形、
よって、OE=4cmと分かります。△ODO'=1/2×DO'×OE=1/2×OO'×DF
1/2×6×4=1/2×5'×h
よって、h=24/5=4.8cmとなります。従って、
△ABO+△DOC
=1/2×AB×h+1/2×CD×h
=1/2×(AB+CD)×h
=1/2×13×4.8
=31.2cm2
(その他の解法)
- 余弦定理、正弦定理、三角関数の倍角定理等を駆使して解く ・・・
中村明海さん、sodoさん、M.Hossieさん、有無相生さん、他