第255問の解答
1.問題 [速さの問題]
|
ある川の上流のA港にマサルさん、下流のB港にトモエさんがいます。2人はモーターボートに乗ってA港とB港の間を1往復することにしました。 まず、トモエさんが出発し、その●分後にマサルさんが出発します。2人はともに、目的地に到着すると■分間休んでから反対方向に出発します。すると、2人が2度目に出会った地点は、A港とB港を3:2に分ける点で、B港寄りであったそうです。 また、もしもマサルさんが休憩なしで往復していたなら、2人が2度目に出会う地点と1度目に出会う地点は同じになっていたということです。 このとき、●と■の比を求めてください。 ただし、2人の乗るモーターボートは同じで、上流から下流に向かうときには時速50km、下流から上流に向かうときには時速30kmの速度が出るものとします。 |
2.解答例1(長野美光さん、中村明海さん、数楽者さん、ふじさきたつみさん、高橋道広さん、トトロ@Nさん、大野稔さん、他多数)
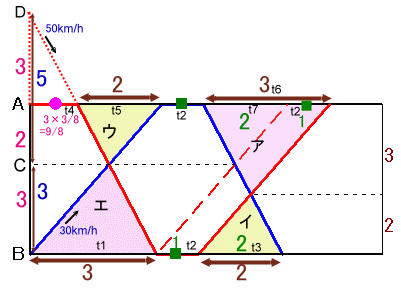
下図のようなダイアグラムで考えます。
2度目に出会ったのがAB間を3:2で分ける点なので、アとイの三角形は相似で相似比は3:2。
よって、t6(=t7+t2):t3=3:2。AからB、およびBからAへの速度はそれぞれ一定なので、t1=t2+t7=t6、t5+t2=t2+t3。
よって、t1=t6=3、t5=t3=2。従って、ウとエの三角形は相似で相似比は2:3。
すなわち、AC:CB=2:3。また、マサルさんがBで休憩なしに往復すると、C地点で再び出会うことから、t1=t2+t3。
よって、■=t2=t1−t3=1。マサルさんが最初に●分間休憩する替わりに、上流のD地点から出発したものとすると、最初に出会うまでの時間に2人が進んだ距離は速度に反比例するので、DC:CB=5:3。
よって、DA=3となります。従って、●=t7=t1×3/8=9/8。
よって、●:■=9/8:1=9:8。答:9:8
以上
3.解答例2(小杉原啓さん、有無相生さん、他)
AB間の距離=750L(km)とします。
AC=450L、BC=300Lとなります。
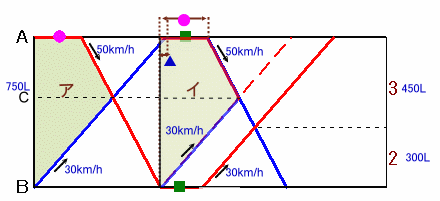
2度目に出会うまでの時間は、
マサルさん:●+750L/50+■+300L/30
トモエさん:750L/30+■+450L/50すなわち、
●+■+25L=■+34L
よって、●=34L−25L=9Lまた、最初にトモエさんがA港に着くまでと、マサルさんがB港に着くまでの時間差を▲とします。
●+750L/50+▲=750L/30
よって、▲=25L−(9L+15L)=Lところで、四角形アとイは題意から合同であることから、
■=●−▲=9L−L=8L
従って、●:■=9L:8L=9:8。