第２５６問の解答

１．問題　［平面図形］

問題図
左図のような三角形ＡＢＣがあり、辺ＡＢを一辺とする平行四辺形ＡＢＱＰと辺ＡＣを一辺とする平行四辺形ＡＣＳＲをそれぞれ三角形ＡＢＣの外側に作りました。

また、直線ＱＰと直線ＳＲが交わった点をＴ、直線ＴＡが辺ＢＣと交わった点をＥとします。すると、ＢＥ：ＥＣ＝４：３となりました。

三角形ＡＢＣの面積が５６cm2、平行四辺形ＡＢＱＰの面積は４８cm2であるとき、平行四辺形ＡＣＳＲの面積は何cm2でしょうか。

２．解答例１（小杉原啓さん、中村明海さん、AUさん、M.Hossieさん、Michaelさん、他多数）

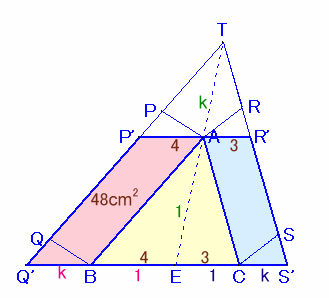
Ａを通り辺ＢＣに平行に引いた直線と辺ＴＱ、および辺ＴＳとの交点をＰ'、Ｒ'とします。また、辺ＢＣの延長線とＴＱ、およびＴＳの延長線との交点をＱ'、Ｓ'とします。

参考図1

平行四辺形ＡＢＱＰとＡＢＱ'Ｐ'は、底辺が共通（共通）で、高さが等しいので、　平行四辺形ＡＢＱＰ＝平行四辺形ＡＢＱ'Ｐ'＝４８ｃｍ2。
同様に、
　平行四辺形ＡＣＳＲ＝ＡＣＳ'Ｒ'。

△ＥＡＢ∽△ＥＴＱ'より、ＡＥ：ＡＴ＝１：ｋとすると、
　ＢＥ：ＢＱ'＝ＡＥ：ＡＴ＝１：ｋ。

同様に、△ＥＡＢ∽△ＥＴＱ'より、
　ＥＣ：ＣＳ'＝ＡＥ：ＡＴ＝１：ｋ。

ＢＱ'：ＣＳ'＝ＢＥ×ｋ：ＥＣ×ｋ＝ＢＥ：ＥＣ＝４：３。

平行四辺形ＡＢＱ'Ｐ'と平行四辺形ＡＣＳ'Ｒ'は、底辺の比が４：３で高さが共通、よって、平行四辺形ＡＢＱ'Ｐ'：平行四辺形ＡＣＳ'Ｒ'＝４：３。

従って、平行四辺形ＡＣＳ'Ｒ'＝平行四辺形ＡＢＱ'Ｐ'×３/４＝３６ｃｍ2。
よって、平行四辺形ＡＣＳＲ＝平行四辺形ＡＣＳ'Ｒ'＝３６ｃｍ2。

答：３６ｃｍ2

以上

３．解答例２（長野美光さん、ミミズクはくず耳さん、Gouさん、他多数）

点Ｂを通り辺ＥＴに引いた直線と辺ＰＱの交点をＱ'、および点Ｃを通り辺ＥＴに平行に引いた直線と辺ＲＳの交点をＳ'とします。

参考図2

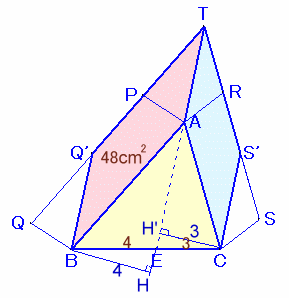
平行四辺形ＡＢＱＰと平行四辺形ＡＢＱ'Ｔは、底辺が共通（ＡＢ）で高さが等しいので、平行四辺形ＡＢＱＰ＝平行四辺形ＡＢＱ'Ｔ。

同様に、平行四辺形ＡＣＳＲ＝平行四辺形ＡＣＳ'Ｔ。

さて、点Ｂ、および点Ｃから直線ＴＥに下ろした垂線の足をＨ、Ｈ'とします。
△ＥＢＨ∽△ＥＣＨ'より、ＢＨ：ＣＨ'＝ＢＥ：ＥＣ＝４：３。

平行四辺形ＡＢＱ'Ｔと平行四辺形ＡＣＳ'Ｔは、底辺が共通（ＴＡ）で高さの比がＢＨ：ＣＨ'＝４：３。
よって、平行四辺形ＡＢＱ'Ｔ：平行四辺形ＡＣＳ'Ｔ＝４：３。
平行四辺形ＡＣＳ'Ｔ＝平行四辺形ＡＢＱ'Ｔ×４/３＝３６ｃｍ2。

従って、平行四辺形ＡＣＳＲ＝平行四辺形ＡＣＳ'Ｔ＝３６ｃｍ2。

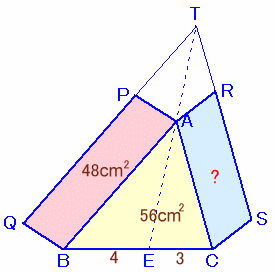
４．解答例３（多数）

ほぼ、解答例１と同様です。

参考図3

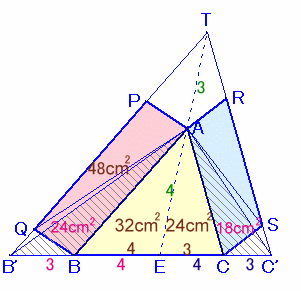
△ＡＢＥ：△ＡＥＣ＝ＢＥ：ＥＣ＝４：３。
よって、△ＡＢＥ＝５６×４/７＝３２ｃｍ2、△ＡＥＣ＝５６×３/７＝２４ｃｍ2。

△ＡＢ'Ｂ＝△ＡＱＢ＝平行四辺形ＡＢＱＰ×１/２＝２４ｃｍ2。
従って、Ｂ'Ｂ：ＢＥ＝△ＡＢ'Ｂ：△ＡＢＥ＝２４：３２＝３：４。

ＣC'：EC＝AT：EA＝BB'：EB＝３：４。
よって。△ACC'=△AEC×３/４＝２４×３/４＝１８ｃｍ2。

従って、平行四辺形ACSR＝△ＡＣＳ×２＝△ＡＣＣ'×２＝３６ｃｍ2。

（他の解法）
ほぼ全員が、等積変形および相似等を使って解かれたようです　・・・
トトロ＠Ｎさん、永井暁さん、ちーくん、うっしーさん、ＫＩＮさん、ぶるぼんさん、鉄老さん、DrKさん、角田鉄也さん、他