第２５７問の解答

---

１．問題　［空間図形、平面図形］

左図のような三角錐ＡＢＣＤがあります。 この三角錐は、ＡＢ＝９cm、ＡＣ＝１５cm、ＡＤ＝１６cm、ＢＣ＝１２cm、∠ＡＢＣ＝９０度となっています。 また、∠ＢＡＣ＝∠ＣＡＤで、頂点Ａに集まる３つの角の和は１８０度になっています。 では、三角錐ＡＢＣＤの表面積は何cm2でしょうか。

---

２．解答例１(ヒデー王子さん、小杉原啓さん、トトロ＠Ｎさん、まるケンさん、他)

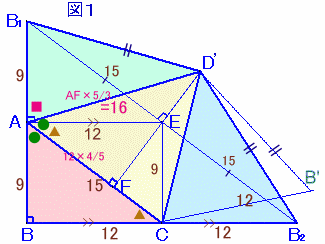
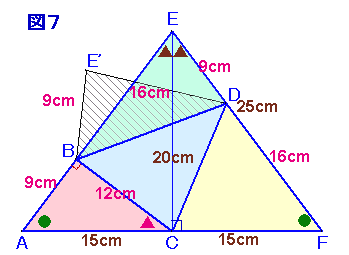
三角錐の展開図を△ACDを中心に書くと、図１のようになる。

ここで、∠BAC＋∠CAD＋∠ABD＝１８０度だから、B、A、B₁は１直線上にある。
また、B、C、B₂も１直線上に並ぶように見えますが、それを直接証明することは難しい。

(B、C、B₂が１直線上にあること)
そこで、B₂は、辺BCの延長上にCB₂＝BC＝9cmにとり、D'を直線AD(またはその延長線)上にD'B₁＝D'B₂となるようにとる。
また、点EをB₁とB₂の中点、DEを延長しACとの交点をFとする。

D'B₁＝D'B₂より、D'はB₁B₂の垂直２等分線上にあるので、D'EとB₁B₂は直交する。
また、B₁B₂はACと平行より、D'FもACに直交する。

中点連結定理より、AEはBB₂に平行でAE＝BB₂×1/2＝BC＝12cm。
同様にECは、BB₁に平行でEC＝AB＝9cm。

従って、△AEF∽△CABとなり、AF＝AE×4/5＝12×4/5。
また、△D'AF∽△CABとなり、AD'＝AF×5/3＝12×4/5×5/3＝16cm。

よって、D'はDと一致する。

さてここで、もし実際のB₂がBCの延長線上になく、別の位置B'にあると仮定する。
すると、D'B'＝B1D'＝D'B₂、CB'＝CB₂＝12cm、CD'は共通と３辺が等しくなり、△D'CB'≡△D'CB₂。
すなわち、これはB'がB₂と異なることに反する。
よって、B、C、B₂は１直線上に並びます。

(三角錐の表面積)
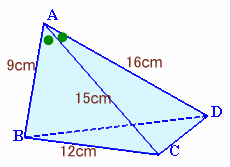
図２で考えます。
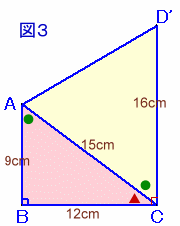
△ABC＝1/2×9×12＝54cm²。
△ACD＝1/2×15×(16×4/5)＝96cm²。
よって、四角形ABCD＝△ABC＋△ACD＝54＋96＝150cm²。

なお、図３のように△ＡＣＤをひっくり返すと、台形になり、
面積は1/2×（9+16）×12＝150cm²と求まります。

　

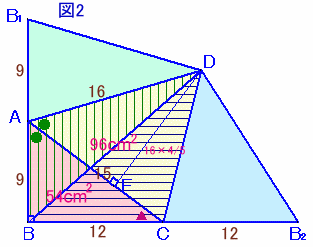
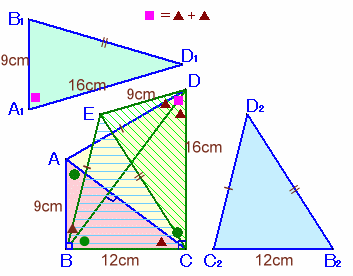
ここで、四角形ABCDを△DBAと△DBCに分割する。
すると、△DB₁Aと△DBAは底辺が9cmで等しく高さが共通より、面積は等しい。
同様に、△DCB₂と△DCBは底辺が12cmで等しく高さが共通より、面積は等しい。
よって、△DB1A＋△DCB2＝△DBA＋△DCB＝150cm²。

以上から、求める表面積は150×2＝300cm²。

答：300ｃｍ²

以上

---

３．解答例２

図１の展開図で、△ＡＢ_１Ｄを裏返して、辺ＡＤを辺ＡＢと平行に、点Ｂ_１を点Ｄにくっつけるように移動します（図４）。

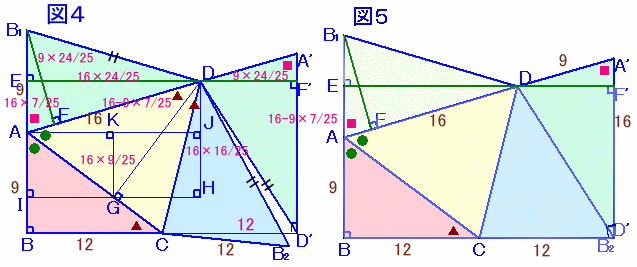
（△ＡＢ_１Ｄを移動して台形を作る）
α＝∠ＢＣＡ、β＝∠ＢＡＣ、γ＝∠Ｂ１ＡＤとおきます。
γ＝１８０度−２β＝２α。
よって、三角関数の倍角公式より、
sinγ＝sin２α＝２sinαcosα＝２×3/5×4/5＝24/25、
cosγ＝cos²α−sin²α＝(4/5)²−(3/5)²＝7/25。
これより、ＡＥ＝ＡＤsinγ＝16×7/25、ED＝ADcosγ＝16×24/25。
B₁F＝ＡＢ_１sinγ＝9×24/25、AF＝AB₁cosγ＝9×7/25、
ＦＤ＝ＡＤ−ＡＦ＝16−9×7/25。

以上を算数的に考えると、次のようになります。
ＡＧ＝ＡＤ×3/5＝16×3/5、ＪＨ＝ＫＧ＝ＡＧ×3/5＝16×9/25。
ＤＧ＝ＡＤ×4/5＝16×4/5、ＤＨ＝ＤＧ×4/5＝16×16/25。
よって、ＡＥ＝ＤＪ＝ＤＨ−ＪＨ＝16×16/25−16×9/25＝16×7/25。
ＩＧ＝ＡＧ×4/5＝16×12/25、ＧＨ＝ＤＧ×3/5＝16×12/25、
よって、ＥＤ＝ＩＧ＋ＧＨ＝16×24/25。
Ｂ_１Ｆ＝ＡＢ_１×ＥＤ/ＡＤ＝9×24/25、ＡＦ＝ＡＢ１×ＡＥ/ＡＤ＝9×7/25、
ＦＤ＝ＡＤ−ＡＦ＝16−9×7/25。

さて、ＤＦ'はＡ'Ｄ'と直交しているので、ＡＢとも直交、
よって、Ｅ、Ｄ、Ｆ'は１直線上に並びます。

また、Ｆ'Ｄ'＝ＦＤ＝16−9×7/25＝337/25、ＥＢ＝ＡＢ＋ＡＥ＝9＋16×7/25＝337/25。
よって、Ｆ'Ｄ'＝ＥＢ。従って、Ｄ'はＢＣの延長線上にあります。

さらに、ＥＦ'＝ＥＤ＋Ｂ_１Ｆ＝16×24/25＋9×24/25＝（16+9）×24/25＝24、
従って、ＢＤ'＝ＥＦ'＝24、CD'＝ＢＤ'−ＢＣ＝24-12＝１２。

すると、ＤＤ'＝ＤＢ₂、ＣＤ'＝ＣＢ₂より、△ＤＣＤ'≡△ＤＣＢ₂。
よって、Ｄ'とＢ₂は一致します。

また、∠Ａ'ＤＦ'＝９０度−γ＝∠ＡＤＥ、よってＡ、Ｄ、Ａ'は１直線上にあります。
以上から、求める三角錐の表面積は、台形Ａ'ＡＢＤ'の面積に等しく、
　1/2×（9+16）×24＝300cm²となります。

答：300ｃｍ²

以上

---

４．解答例３（ミミズクはくず耳さん、まるケンさん、他）

まず、三角錐は一意的に決まることに注意しましょう。
何故なら、題意より△ＡＢＣ、△ＡＣＤ、△ＡＤＢとも、２辺とこれを挟む角が決まっていますので、それぞれ一意的に決まります。
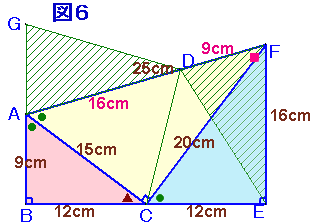
すると△ＢＣＤの３辺が決まるので、これも一意的に決まります。

さて、図６のように辺の長さが３：４：５の直角三角形に相似な３種類の三角形をくっつけます。すなわち、△ABCは、３×３：３×４：３×５、△ＣＥＦは４×３：４×４：４×５、△ACFは４×３：４×４：４×５になっています。

すると、∠ＡＣＢ＋∠ＡＣＦ＋∠ＦＣＥ＝（∠ＡＣＢ＋∠ＦＣＥ）＋∠ＡＣＦ
　＝（∠ＡＣＢ＋∠ＣＡＢ）＋９０度＝９０度＋９０度＝１８０度。
よって、Ｂ、Ｃ、Ｅは１直線上に並びます。
ＦＥ、ＡＢとも辺ＢＥに直交するので、四角形ＡＢＤＦは台形となります。
ちなみに、この台形の面積は、1/2×（9+16）×24＝３００cm²です。

ここで、辺ＡＦ上にＡＤ＝１６ｃｍとなるように点Ｄをとります。ＤＦ＝ＡＦ−ＡＤ＝９ｃｍ。
そして、△ＥＦＤを裏返して点Ｅを点Ｄに、点Ｆを点Ａにくっつけるように移動し、点Ｄが移動したものを点Ｇとします。

ＡG＝ＤＦ＝９ｃｍ＝ＡＢ、ＢＣ＝ＣＥ＝１２ｃｍ、ＧＤ＝ＤＥ、ＡＤ＝１６ｃｍであることから、△ＧＡＤ、△ＡＢＣ、△ＤＣＥ、△ＡＣＤを合わせた図形は、ある三角錐の展開図になっています。

ところで、∠ＧＡＤ＋∠ＤＡＢ＝∠ＤＦＥ＋∠ＤＡＢ＝１８０度、よってＢ、Ａ、Ｇは１直線上に並びます。従って、図６の四角形ＧＢＥＤは、本題の三角錐の展開図の一つになります

先に示したように三角錐は一意的に決まりますので、
求める表面積は、四角形ＧＢＥＤ＝台形ＡＢＤＦ＝３００cm²となります。

---

４−２．解答例３−２（Mr.Xさん）・・・追加しました

三角錐の４つの面をばらして、△ACDを裏返しにし、△ABCの辺ACに合わせます。

題意より∠ACD＝∠BACだから、
　∠BCD＝∠BCA＋∠ACD
　　　　　＝∠BCA＋∠BAC
　　　　　＝９０度。
従って、四角形DABCは台形となります。

BC＝９ｃｍ、ＣＤ＝１２ｃｍより、△ＢＣＤ∽△ＡＢＣ、
よって、∠ＢＤＣ＝∠ＡＣＢ＝∠ＡＢＤ。　

さて、頂点Ｄから∠ＥＤＢ＝∠ＢＤＣとなるように直線を引き、ＤＥ＝ＡＢ＝９ｃｍとします。

△ＥＤＢと△ＡＢＤについて、ＥＤ＝ＡＢ、ＢＤは共通、∠ＥＤＢ＝∠ＡＢＤだから
二辺挟角が等しいので合同。
よって、ＥＢ＝ＡＤ＝Ｄ₂Ｃ₂。

△ＥＤＣと△Ｂ₁Ａ₁Ｄ₁について、ＥＤ＝Ａ₁Ｂ₁＝９ｃｍ、ＤＣ＝Ａ₁Ｄ₁＝１６ｃｍ、
∠ＥＤＣ＝２×∠ＢＤＣ＝２×（９０度−∠ＢＡＣ）＝∠Ｂ₁Ａ₁Ｄ₁となり、
二辺挟角が等しいので合同。
よって、ＥＣ＝Ｂ₁Ｄ₁＝Ｄ₂Ｂ₂。

△ＥＢＣと△Ｄ₂Ｃ₂Ｂ₂について、ＥＢ＝Ｄ₂Ｃ₂、ＥＣ＝Ｄ₂Ｂ₂、ＢＣ＝Ｃ₂Ｂ₂＝１２ｃｍとなり、
三辺が等しいので合同。

従って、△Ｂ₁Ａ₁Ｄ₁＋△Ｄ₂Ｃ₂Ｂ₂
　＝△ＥＤＣ＋△ＥＢＣ
　＝四角形ＤＥＢＣ
　＝四角形ＤＡＢＣ。

従って、三角錐の表面積
　＝２×四角形ＤＡＢＣ
　＝２×1/2×（９＋１６）×１２
　＝３００cm²

---

５．解答例４（マサルさん、ヘロン久野さん、他）

図７のように、辺の長さが１５：２０：２５の直角三角形ＡＣＥとＦＣＥを合わせて二等辺三角形ＥＡＦを作ります。この面積は、１５×２０＝３００ｃｍ²です。

辺ＥＡ上にＥＢ＝１６ｃｍとなるように点Ｂを、辺ＥＦ上にＥＤ＝９ｃｍとなるよう点Ｄをとります。そして、△ＥＢＤを裏返して、点Ｂを点Ｄに、点Ｄを点Ｂにくっつけるよう移動します。
このとき、点Ｅが移動した先をＥ'とします。

すると、ＡＢ＝ＢＥ'＝９ｃｍ、ＡＣ＝ＦＣ＝１５ｃｍ、ＦＤ＝Ｅ'Ｄ＝１６ｃｍとなり、
これらは△ＢＣＤを底辺とする三角錐の展開図になっていることが分かります。

さて、△ＡＢＣと△ＡＣＥは、ＡＢ：ＡＣ＝９：１５＝３：５、ＡＣ：ＡＥ＝１５：２５＝３：５、
∠ＢＡＣと∠ＣＡＥは共通より、△ＡＢＣ∽△ＡＣＥ。
よって、△ＡＢＣは辺の長さが９：１２：１５の直角三角形となります。

また、∠ＢＡＣ＝∠ＣＦＤ、∠ＢＡＣ＋∠ＣＦＤ＋∠ＢＥＤ＝２×（∠ＢＡＣ＋∠ＢＥＣ）＝１８０度となり、図７が本題の三角錐の展開図となることが分かります。

従って、求める表面積＝△ＥＡＣ＝３００ｃｍ²。

---

６．解答例５（高田修成さん、ハラギャーテイさん、有無相生さん、M.Hossieさん、a_pepperさん、他多数）

図８のように、α、β、γをとります。
sinα＝cosβ＝3/5、cosα＝sinβ＝4/5。

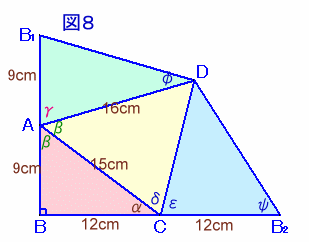
題意より、
　γ＝１８０度−２β＝２×（９０−β）＝２α、
よって、倍角公式より、
　sinγ＝sin２α＝２sinαcosα＝2×3/5×4/5＝24/25、
　cosγ＝cos２α＝cos²α−sin²α＝(4/5)²−(3/5)²＝7/25。

余弦定理より、
　Ｂ₁Ｄ＝√（９²＋１６²−２・９・１６・cosγ）＝（√6409）/5
　ＣＤ＝√（１５²＋１６²−２・１５・１６・cosβ）＝√193。

正弦弦定理より、
　sinδ/ＡＤ＝sinβ/ＣＤ、
よって、
　sinδ＝ＡＤ/ＣＤ・sinβ＝16/√193×4/5＝(64/965)√193、
　cosδ＝√（１−sin²δ）＝(27/965)√193。
また、余弦定理より、
　cosε＝（CD²＋１２²−B₂D²）/（２・CD・１２）
　　＝（193＋144−6409/25)/(24√193)
　　＝(84/4825)√(193)。
　sinε＝√(1-cos²ε)＝(337/4825)√193。

従って、
△ＡＢＣ＝1/2×９×１５×sinβ＝1/2×９×１５×4/5＝５４cm²
△ＡＣＤ＝1/2×１６×１５×sinβ＝1/2×１６×１５×4/5＝９６cm²
△ＡＢ₁Ｄ＝1/2×９×１６×sinγ＝1/2×９×１６×24/25＝1728/25cm²
△ＤＣＢ₂＝1/2×１２×ＣＤ×sinε＝1/2×１２×√193×(337/4825)√193＝2022/25cm²
よって、求める三角錐の表面積
　＝△ＡＢＣ＋△ＡＣＤ＋△ＡＢ₁Ｄ＋△ＤＣＢ₂
　＝54＋96＋1728/25＋2022/25
　＝150＋150
　＝300cm²
と分かります。

　

（参考）Ｂ、Ｃ、Ｂ₂が、一直線上に並ぶこと

cos(α+δ)＝cosαcosδ−sinαsinδ
　　＝4/5・(27/965)√193−3/5・(64/965)√193
　　＝-(84/4825)√193。

従って、cos(α+δ)＝−cosεとなり、
0<α+δ<１８０度、0<ε<１８０度から、（α+δ）＋ε＝１８０度が成り立ち、
Ｂ、Ｃ、Ｂ₂は一直線上に並ぶことが分かります。

（参考）∠ＡＢ₁Ｄ＋∠ＣＢ₂Ｄ＝９０度となること

正弦弦定理より、
　sinφ/ＡＢ₁＝sinγ/Ｂ₁Ｄ、
よって、
　sinφ＝ＡＢ₁/Ｂ₁Ｄsinγ
　　＝9/(（√6409）/5)・24/25
　　＝(216/32045)√6409

　sinψ/ＣＤ＝sinε/ＤＢ₂、
よって、
　sinψ＝ＣＤ/ＤＢ₂sinε
　　＝√193/(（√6409）/5)・(337/4825)√193
　　＝(337/32045)√6409

従って、sin²φ＋sin²ψ＝(216²+337²)/32045²・6409＝１となり、
図８より、0<φ<90度、0<ψ<90度から、φ+ψ＝９０度が成り立ちます。

---