第２５８問の解答

１．問題　［空間図形］

問題図
左図は、全ての辺が直線でできた立体の「真上から見た図」と「正面から見た図」を表していて、両者は全く同じになっています。（“隠れ辺”はありません）

どちらの図も、外側の大きな正方形は一辺の長さが６cm、内側の小さな正方形は一辺の長さが４cmとなっています。

このとき、この立体の体積を求めてください。なお、この立体として複数考えられる場合は、最も体積の大きいものを答えてください。

２．解答例１(トトロ＠Ｎさん、ミミズクはくず耳さん、ＡЯＯＴさん、長野美光さん、鉄老さん、M.Hossieさん、他多数)

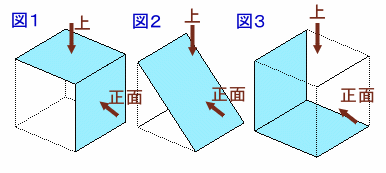
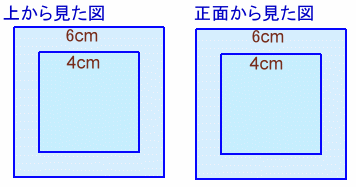
全ての辺が直線であることから、「真上から見た図」と「正面から見た図」が正方形となるのは、下記の３ケースと考えられます。

参考図1

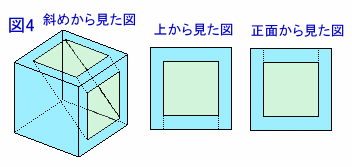
６ｃｍの正方形のについて、図１では真ん中に４ｃｍの正方形が来るのは、中をくり抜く必要があるため、隠れ線が存在するため不適（例：図４）。
図３は、体積が０となり、図２の場合より小さくなるので不適。

参考図2

よって、題意を満たすのは図２のケースと考えられる。
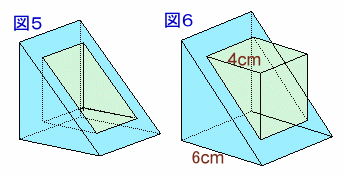
さらに、４ｃｍの正方形の場合を考えると、図５または図６の２ケースあり、体積が大きいのは図６の場合である。

参考図3

図６は、６ｃｍ、４ｃｍの２つの立方体の半分である三角柱をくっつけた形となっているので、
　体積＝1/2×63＋1/2×43
　　　　＝108＋32
　　　　＝140cm3
となります。

答：140ｃｍ3

以上