第259問の解答
1.問題 [平面図形]
|
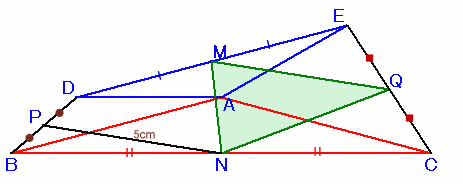
上図のような四角形DBCEがあります。 この四角形の内部に点Aをとったところ、△ABC、△ADEはいずれも∠A=150度の二等辺三角形になりました。 ここで、四角形DBCEの4つの辺のそれぞれの中点P、N、Q、Mをとります。 すると、PN=5cmとなったそうです。 では、△QMNの面積は何cm2でしょうか。 |
2.解答例1(医学部性さん、長野美光さん、名倉っちさん、小杉原啓さん、M.Hossieさん、武田浩紀さん、高橋道広さん、有無相生さん、あやのりんさん、他多数)
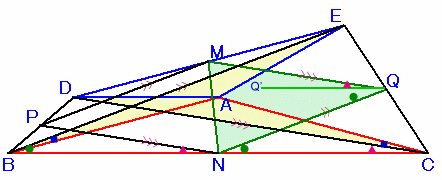
(四角形MPNQが平行四辺形となること)
△DBEにおいて、中点連結定理により、
PMとBEは平行で、PM=BE×1/2。
△CEBにおいて、中点連結定理により、
NQとBEは平行で、NQ=BE×1/2。
よって、PMとNQは平行かつPM=NQ=BE×1/2。同様にして、PNとMQは平行かつPN=MQ=DC×1/2。
なので、四角形MPNQは平行四辺形となる。
(四角形MPNQは菱形となること)
△AEBと△ADCについて、 AE=AD、AB=AC、および
∠BAE=∠DAE+∠DAB=∠BAC+∠DAB=∠CAD
よって、二辺挟角が等しいので△AEB≡△ADC。従って、BE=DC。
よって、PM=NQ=PN=MQ=5cmとなることから、四角形MPNQは菱形となります。(∠MQN=30度となること)
∠MQQ'=∠QNC=∠EBC、∠Q'QN=∠PNB=∠DCB。
よって、
∠MQN
=∠MQQ'+∠Q'QN
=∠EBC+∠DCB
=(∠ABC+∠EBA)+(∠ACB−∠ACD)
=∠ABC+∠ACB (∵∠EBA=∠ACD)
=180度−∠BAC
=30度。(△QMNの面積)
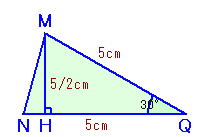
点Mから辺NQに下ろした垂線の足を点Hとします。
∠MQN=30度より、MH=MQ×1/2=5/2cm、
よって、△QMN=1/2×5×5/2=25/4cm2。答:25/4cm2
以上
(その他の解法)
・四角形DBCEが長方形となる特別の場合で考える ・・・
トトロ@Nさん、あんみつさん、CRYING DOLPHINさん、a_pepperさん、Mikiさん、ミミズクはくず耳さん、
C_GUMさん、Gouさん、ハラギャーテイさん、他