第262問の解答
1.問題 [空間図形]
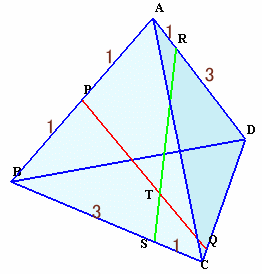 |
(参考) 3D図 |
2.解答例1(辻さん、ヌオの母さん、Mikiさん、有無相生さん、Nagahiroさん、M.Hossieさん、アークさん、村田耕一朗さん、DrKさん、他多数)
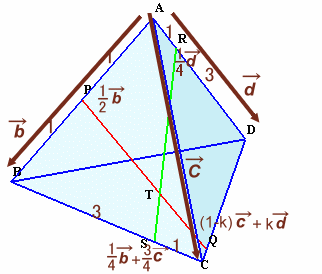
頂点A を始点にして、空間ベクトルをb→=AB→、c→=AC→、d→=AD→の1次式で表現することにします。
また、CQ:QD=k:(1-k)、PT:TQ=s:(1-s)、ST:TR=t:(1-t) とおきます。
すると、
AP→=1/2b→、AQ→=(1-k)c→+kd→、AR→=1/4d→、
AS→=1/4b→+3/4c→
および
AT→=(1-s)AP→+sAQ→
= (1-s)・1/2b→+s{(1-k)c→+kd→}
=(1-s)/2b→+s(1-k)c→+skd→ ・・・(1)
そして、
AT→=(1-t)AS→+tAR→
=(1-t){1/4b→+3/4c→}+t・1/4d→
=(1-t)/4b→+3(1-t)/4c→+t/4d→ ・・・(2)
と表せます。ここで、b→、c→、d→は線形独立なので、 (1)、(2)より
(1-s)/2 = (1-t)/4 、s(1-k)=3(1-t)/4 、sk=t/4
が成り立ちます。これらを解くと、 k=1/10、s=5/8、t=1/4 が得られます。
よって、CQ:QD=1:9、PT:TQ=5:3となります。
答:(1)1:9 (2)5:3以上
3.解答例2(へロン久野さん、Taroさん、KINさん、みっちんさん、他)
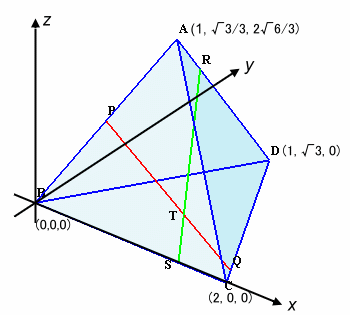
下図のように、BCをx軸にとり、 底面(BCD)をxy平面に置くように設定します。
正四面体の一辺の長さを2とすると、A、B、C、D各点の座標は次のように与えられます。
A(1, √3/3, 2√6/3)、B(0,0,0)、C(2, 0, 0)、D(1, √3, 0)
同様にして、P、R、S各点の座標値は以下のようになります。
P(1/2, √3/6, √6/3)、R(1, √3/2, √6/2)、S(3/2, 0, 0)
線分PQとRSとは点Tで交わるから、PQおよびRSは同一平面上に存在します。そこでその平面の方程式を一般形として次式で表し、その方程式に上記P、R、Sの各点の座標を代入することにより、係数 a、b、c を求めます。
(x/a)+(y/b)+(z/c)=1 ・・・ 一般式
このようにして求めた平面の方程式は下記の様になる。
6x−8√3y+5√6z=9 ・・・ (1)
この平面と線分CDの交わる点が点Q。
ここでCDを通る直線の方程式は
y=-√3x+2√3 ・・・ (2)
また、点Qのz座標は0であるから、残りのx座標とy座標を(1)、(2)より求めれば、
x=19/10、y=√3/10
を得ます。よって、点Qの座標は(19/10, √3/10, 0)となります。
従って、 CQ:QD=1:9 ・・・ 設問1の答
点Qの座標が求まったので、後はPQとRSをそれぞれxy平面に投影させて交点Tを求めます。投影時のそれぞれの直線の方程式は
PQ: y=-(√3/21)x+4√3/21 ・・・ (3)
RS: y=−√3x+3√3/2 ・・・ (4)
となるので、(3)、(4)より、
x=11/8、y=√3/8
を得ます。よって、点Tのxy平面への投影点T'の座標は(11/8, √3/8)と分ります。
従って、点P、T'、Qの各x座標間の距離の比が、そのままPTとQTの長さの比となるから、これを計算して
PT:TQ=5:3 ・・・ 設問2の答
を得ます。
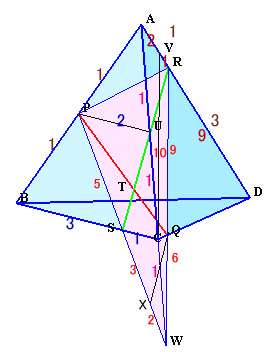
4.解答例3(AЯOTさん、摩天楼さん、CRYING DOLPHINさん、高橋道広さん、ふじさきたつみさん、ノーザンビレッジさん、ヒデー王子さん、他多数)
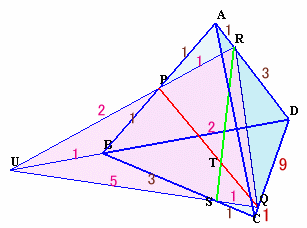
点P、Q、R、Sは同一平面上にあります。
この平面と直線DBの交点をUとすると、直線RP、QSはともに点Uを通ります。
△ABDと直線RUに関してメネラウスの定理より、
(AP/PB)・(BU/UD)・(DR/RA)=1
(1/1)・(BU/UD)・(3/1)=1
BU/UD=1/3
よって、DB:BU=2:1。△RUDと直線ABに関してメネラウスの定理より、
(RP/PU)・(UB/BD)・(DA/AR)=1
(RP/PU)・(1/2)・(4/1)=1
RP/PU=1/2
よって、RP:PU=1:2。△DBCと直線UQに関してメネラウスの定理より、
(DU/UB)・(BS/SC)・(CQ/QD)=1
(3/1)・(3/1)・(CQ/QD)=1
CQ/QD=1/9
よって、CQ:QD=1:9。 ・・・ 設問1の答△UQDと直線BCに関してメネラウスの定理より、
(US/SQ)・(QC/CD)・(DB/BU)=1
(US/SQ)・(1/10)・(2/1)=1
US/SQ=5
よって、US:SQ=5:1。△UQPと直線SRに関してメネラウスの定理より、
(US/SQ)・(QT/TP)・(PR/RU)=1
(5/1)・(QT/TP)・(1/3)=1
QT/TP=3/5
よって、PT:TQ=5:3。 ・・・ 設問2の答
5.解答例4(あやのりんさん、他)
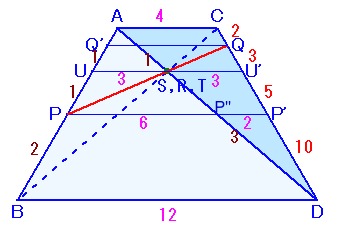
点Sと点Rが重なるようにしてSの方から見て、以下はこの方向に垂直な平面に投影した点について考えることにします。
AR:RD=CS:SB=1:3、およびAD=BCより四角形ABDCは台形になります。
すると、BP:PA=1:1、BU:UA=DS:SA=3:1より、
BP:PU:UA=2:1:1。さて、△ASC∽△SBDで相似比は1:3、
よって、BD=12とおくとAC=BD×1/3=4となります。点Pを通ってBDと平行に引いた直線とCDの交点をP'、ADとの交点をP''
点Sを通ってBDと平行に引いた直線とABの交点をU、CDとの交点をU'、
および点Qを通ってBDと平行に引いた直線とABの交点をQ'とします。△APP''∽△ABD、AP:PB=1:1よりPP''=BD×1/2=6。
△AUS'∽△ABD、AU:UB=1:3よりUS=BD×1/4=3。
△DPP''∽△DAC、DP'':PC=1:1よりP''P'=AC×1/2=2。
△DSU'∽△DAC、DS:SC=1:3よりSU'=AC×3/4=3。さらに、
△QSU'∽△QPP'、SU':PP'=3:8より、
PT:TQ=U'P':QU'=5:3。 ・・・ 設問2の答U'P'=5とおくと、QU'=3。
CU'=U'P'=5より、CQ=CU'−QU'=2。
P'D=CP'=10。よって、CQ:QD=2:18=1:9。・・・ 設問2の答
6.解答例5(高橋道広さん、トトロ@Nさん、他)
平面PSQRと直線ACの交点をWとします。
AC上にBCとPUが平行となる点Uをとります。BC:PU=4:2より、SC:PU=1:2。
よって、中点連結定理より、WC:CU=1:1。AP:PB=1:1より、AU:UC=1:1。
従って、AC:CW=2:1次に、AD上にCVとQRが平行になる点Vをとります。
AV:VR=AC:CW=2:1、
ここで、VR=1とすると、AV=2、AR=3。AR:RD=1:3より、RD=9となる
よって、CQ:QD=VR:RD=1:9。 ・・・ 設問1の答
また、PS:SW=UC:CW=1:1。
ここで、QR=9とします。
DR:RV=9:1より、VC=10。AC:CW=2:1より、RW=15、
よって、WQ=RW−RQ=15−9=6、
従って、WQ:QR=6:9=2:3。
QXがSRに平行になるように、PW上に点Xを取ります。
SX:XW=RQ:QW=3:2。ここで、SX=3とすると、XW=2、SW=5。
PS:SW=1:1より、PS=5。
従って、PT:TQ=PS:SX=5:3。 ・・・ 設問2の答
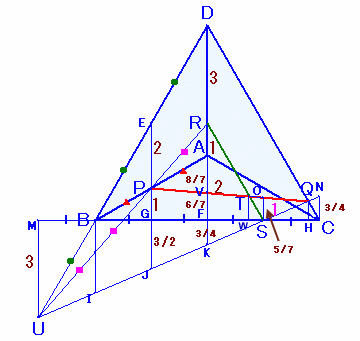
7.解答例6(高田修成さん、馬渕の算数星人さん、tub@saさん、まるケンさん、他)
底面BCDを下に、頂点Aを上にして、真上から見た図を考えます。
AB=AC=ADの長さを3とします。
P、Q、R、Sは同一平面にあるので、RPとQS、およびDBを延長すると、同じ点(Uとします)で交わります。
さらに、上図のように各点をとると、三角形の相似から、
DE=EB=BU、よってEP=2、PG=1、MU=EG=3となります。また、MB=BG=GF=FS=SC(=1とおきます)となるので、
GJ=3/2、FK=NC=3/4。
よって、DK=6+3/4=27/4。△DKQ∽△CKNで、DK:CN=27/4:3/4=9:1。
よって、CQ:QD=1:9。 ・・・ 設問1の答また、FH=FC×1/10=9/5、SH=4/5。
従って、OS=PJ×4/14=5/2×2/7=5/7、
VK=PJ×9/14=5/2×9/14=45/28、
VF=VK−FK=45/28−21/28=24/28=6/7。よって、AV=AF−VF=2−6/7=8/7、
RV=RA+AV=1+8/7=15/7。
従って、FW:WS=RV:OS=15/7:5/7=3:1、
FW=3/4、WS=1/4。よって、PT:TQ=GW:WH=(GF+FW):(WS+SH)
=(1+3/4):(1/4+4/5)=(20+15):(5+16)
=35:21=5:3 ・・・ 設問2の答
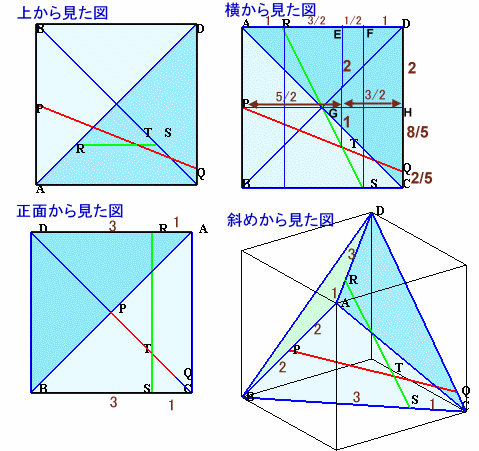
8.解答例7(あんみつさん、他)
ABが下に、CDが上になるように置き、真上から見ると、正方形のように見えます。
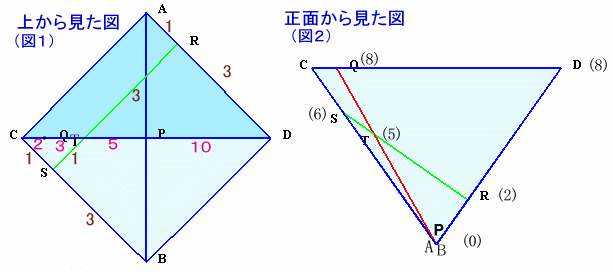
また、ABの中点PとCDの中点が重なって見えます。
そして、AR:RD=CS:SB=1:3だから、RSとACは平行に見えます。さらに、TはRSとPQの交点だから、上図(図1)で△CST∽△TDR、相似比1:3と見えるので、TはPとCのちょうど真ん中にあるように見え ます。
さて、ABのある位置の高さを0、CDのある位置の高さを8と します。
CS:SB=1:3だからSの高さは6、AR:RD=1:3だからRの高さは2、
そして、ST:TR=1:3だから、Tは高さ5にあります。Qは高さ8だから、PT:TQ=5:3。 ・・・ 設問2の答
上図(図1)でTPの長さを5とおくとQT=3、
またCT=TP=5だからCQ=CT−QT=2、PD=CP=10、
従ってCQ:QD=2:18=1:9。 ・・・ 設問1の答
9.解答例8(ぶぶおパパさん、うっしーさん、ミミズクはくず耳さん、他)
正四面体を下図のように立方体に埋め込んで考えます。
上図で、立方体の1辺の長さを4とすると、AR=CS=FD=1、
RF=AD−(AR+FD)=2。RT:TS=DR:SC=3:1となるので、RE:EF=RT:TS=3:1。
よって、RE=3/2、EF=1/2。従って、PT:TQ=PG:GH=5/2:3/2=5:3。 ・・・ 設問2の答
また、ET=FS×3/4=3、GT=ET−EG=1、
HQ=GT×PH/PG=1×(4)/(5/2)=8/5。
CQ=HC−HQ=2/5、QD=HQ+HD=18/5。よって、CQ:QD=2/5:18/5=1:9。 ・・・ 設問2の答
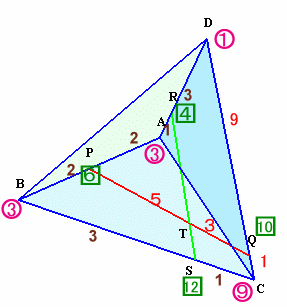
10.解答例9(AЯOTさん、鉄老さん、 他)
点Dに1のおもりを置きます。
点RでA、Dのおもりが釣り合うように、Aに3のおもりを置きます。
(1×3=3×1)点PでA、Bのおもりが釣り合うように、Bに3のおもりを置 きます。
(3×2=3×2)点SでB、Cのおもりが釣り合うように、Cに9のおもりを置 きます。
(3×3=9×1)点QでC、Dのおもりが釣り合うことから、CQ:QD=1:9。 ・・・ 設問2の答
(9×1=1×9)点Qにかかる力は1+9=10、点Pにかかる力は3+3=6 。
よって、点TでP、Qのおもりが釣り合うことから、
PT:TQ=10:6=5:3。(6×5=10×3) ・・・ 設問1の答