第２６４問の解答

１．問題　［空間図形］

問題図
左図は、２７個の部屋に分かれた立方体型の無人マンションを表しています。
いま、３階の一番手前、一番左側にバクダンをしかけたところ、赤く塗られた部屋（全部で７部屋）が破壊されました。
このように、このタイプの無人マンションにバクダンをしかけて爆発させると、
タテ、ヨコ、高さの３方向に爆風がひろがることが分かっています。
また、爆風は何部屋も通過できます。

このとき、
（１）この無人マンションの全部屋を破壊するためには、
　　最低何個のバクダンがいるでしょうか？

（２）７×７×７＝３４３個の部屋に分かれた立方体型の無人マンション
　　の全部屋を破壊するには最低何個のバクダンが必要でしょうか。

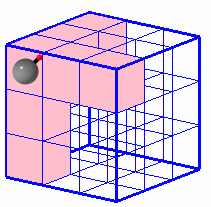２．解答例１(ヒデー王子さん、地蔵さん、長野美光さん、ノーザンビレッジさん、中村明海さん、ちょこさん、ミミズクはくず耳さん、まるケンさん、takuさん、 他多数)

［設問１］
まず、３×３の平面で考えることにしましょう。

参考図１

各行、各列を爆破するのに、それぞれバクダン１個は必要です。
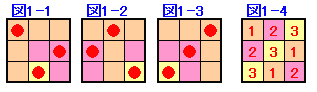
例えば、図１−１のように、同一の行・列には並ばないように配置すると３個のバクダンで平面を爆破することが可能です。

従って、各階には、上下の方向にも重ならないように配置すれば、合計９個のバクダンで爆破できます。

例えば、最上階（階１）に図１−１の配置、真ん中の階（階２）には図１−２のような配置、最下階（階３）には図１−３のような配置でＯＫです。
これを図１−４のように各階に配置するバクダンに番号を付けて表すとわかりやすくなるでしょう。

この方法を完全配置と呼ぶことにします。
完全配置では、ｎ×ｎ×ｎ個の部屋の場合、ｎ2個のバクダンで爆破することができます。

しかしながら、１個のバクダンでは３方向に爆破することができるので、合計３ｎ−２≒３ｎ個の部屋を爆破できるので、もう少し効率的に配置することはできないでしょうか。

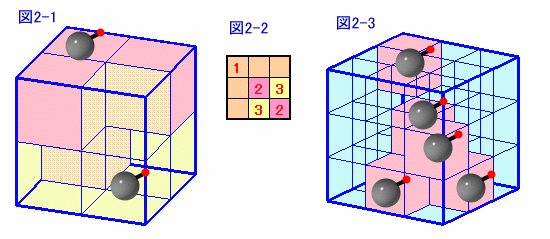
そこで、２×２×２個の部屋の場合を考えてみると、図２−１のように２個のバクダンを対角線上の２部屋に配置するとＯＫです。

参考図２

そこで、これを３×３×３の場合に応用して、図２−２（図２−３）のように配置すれば合計５個で爆破可能です。

さて、４個以下では可能でしょうか。
まず、１個も配置しない階があると、その階の９個の部屋を爆破するため、それ以外の階で合計９個のバクダンが必要ですので不適。

また、各階２個以上配置すると合計６個以上になるのでこれも不適。
よって、１個だけ配置する階が必ずあります。
すると、その階では（図２−２の階１のように）５個の部屋を爆破できますが、残り４個の部屋を爆破するためにあと４個は必要ですので、どうしても５個は最低なければなりません。

［設問２］
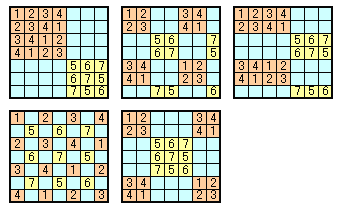
７×７×７の場合も、下図のように配置すれば合計２５個のバクダンで爆破可能です。

一般にｎ×ｎ×ｎ個の場合は、1/2×ｎ2（割り切れないときは切り上げ）で爆破可能のようです。

参考図３

では、２４個以下では可能でしょうか。
もし２個以下の階があると、その階では２行・２列は爆破できても、５×５＝２５個の部屋は残りますので、あと２５個は別の階に必要となり不適。

すべての階が４個以上だと４×７＝２８個以上となり不適。

よって、３個の階が必ずあります。
３個の階では３行・３列は爆破できても４×４＝１６個は残ります。

これを４×４の完全配置にすると、結局上図と同様になり２５個必要です。

もし、４×４の完全配置でなく、この部分には３個しかない階があると、１行・１列は残ってしまうので、２５個でもダメになり不適。

答：（１）５個　（２）２５個

以上