第２６５問の解答

１．問題　［平面図形］

問題図
左図のようなＣＤ＝１０cm、ＤＡ＝６cmの四角形ＡＢＣＤがあります。
  • 頂点Ｂと頂点Ｄ、頂点Ａと頂点Ｃを結んだところ、∠ＣＢＤ＝９０゜、∠ＤＡＣ＝９０゜となりました。
  • ＡＢの中点をＭ、ＣＤの中点をＮとしてこれらを結んだところ、ＭＮ＝４cmとなったそうです。

このとき、ＢＣの長さを求めてください。

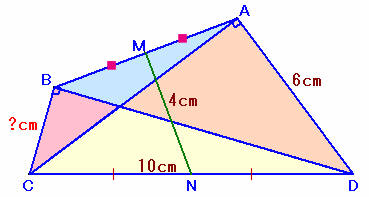２．解答例１(taroさん、 中村明海さん、他)

次の補題を用います。

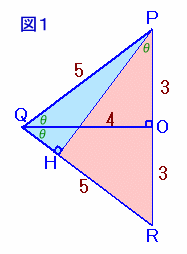
［補題］

辺の長さが３：４：５である直角三角形の最小角をθとします。
２θを含む直角三角形の辺の長さは７：２４：２５である。

参考図１

［証明］

上図のように、辺の長さが３：４：５の直角三角形２個をくっつけます。
また、ＰからＱＲに下ろした垂線の足をＨとします。

　∠ＨＰＲ＝９０度−∠ＰＲＨ＝∠ＲＱＯ
よって、
　ＰＨ＝ＰＲ×４/５＝６×４/５＝２４/５
　ＲＨ＝ＰＲ×３/５＝６×３/５＝１８/５、
　ＱＨ＝ＱＲ−ＲＨ＝５−１８/５＝７/５
従って、
　ＱＨ：ＰＨ：ＰＱ＝７/５：２４/５：５＝７：２４：２５。

あるいは、三角関数の倍角公式を用いて、
　cos2θ＝cos2θ-sin2θ＝(4/5)2−(3/5)2＝7/25
　sin2θ＝2sinθcosθ＝２・(4/5)・(3/5)＝24/25
よって、三辺の比は、
　7/25：24/25：１＝７：２４：２５。

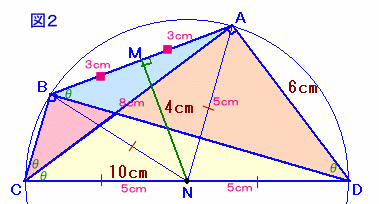
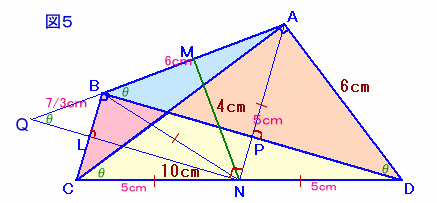
さて、∠ＣＢＤ＝∠ＡＣＤ＝９０度より、点Ａ、Ｂ、Ｃ、Ｄは辺ＣＤを直径とする円周上にあります。

参考図２

点Ｎは辺ＣＤの中点なので、円の中心。
よって、ＮＣ＝ＮＢ＝ＮＡ＝ＮＤ＝５ｃｍ。

△ＮＡＭと△ＮＢＭについて、ＮＡ＝ＮＢ、ＡＭ＝ＢＭ、ＮＭは共通だから、
三辺が等しいので合同。
従って、∠ＡＭＮ＝９０度となり、△ＮＡＭは直角三角形。
ＮＭ＝４ｃｍ、ＮＡ＝５ｃｍだから、ＡＭ＝ＢＭ＝３ｃｍ。

よって、ＡＢ＝ＡＤ＝６ｃｍより、△ＡＢＤは二等辺三角形。
従って、∠ＡＢＤ＝∠ＡＤＢ。　・・・　（１）

さて、円周角より∠ＡＣＤ＝∠ＡＢＤ、∠ＢＣＡ＝∠ＡＤＢ。
（１）より、これらは全て等しい（θとおきます）。

△ＡＢＤは辺の長さが６：８：１０＝３：４：５の直角三角形で、∠ＢＣＤ＝２θ。
よって、補題より、△ＢＣＤの辺の長さが７：２４：２５の直角三角形。

従って、ＢＣ＝ＣＤ×７/２５＝１０×７/２５＝１４/５＝２．８ｃｍ。

答：2.8cm

以上

３．解答例２(トトロ＠Nさん、 ヒデー王子さん、高橋道広さん、他)

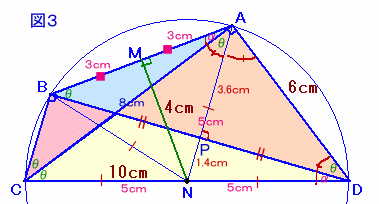
ＡＮとＢＤの交点をＰとします。

参考図３

（１）までは解答例１と同様。

円周角より、∠ＢＡＣ＝∠ＢＤＣ＝α。
△ＮＡＣは二等辺三角形だから、∠ＣＡＮ＝∠ＡＣＤ＝θ＝∠ＡＤＢ。
よって、∠ＢＡＰ＝∠ＡＤＮ＝∠ＤＡＮ（△ＮＡＤは二等辺三角形）。

従って、ＡＰはＢＤの垂直二等分線となります。　・・・　（２）

∠ＡＤＰ＝θより、△ＡＤＰも３：４：５の直角三角形。
よって、ＡＰ＝ＡＤ×３/５＝６×３/５＝３．６ｃｍ。
従って、ＰＮ＝ＡＮ−ＡＰ＝５−３．６＝１．４ｃｍ。

中点連結定理より、ＢＣ＝２×ＰＮ＝２×１．４＝２．８ｃｍ。

４．解答例３(うっしーさん、高橋道広さん、萬田銀次郎さん、他)

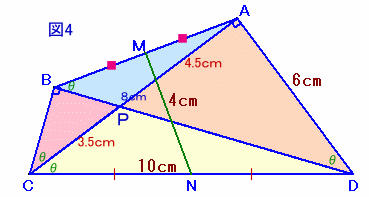
ＡＣとＢＤの交点をＰとします。

参考図４

（１）までは解答例１と同様。

△ＡＰＤ、△ＢＣＰともに３：４：５の直角三角形だから、
ＡＰ＝ＡＤ×３/４＝６×３/４＝４．５ｃｍ。
ＰＣ＝ＡＣ−ＡＰ＝５−４．５＝３．５ｃｍ。
ＢＣ＝ＰＣ×４/５＝３．５×４/５＝２．８ｃｍ。

５．解答例４(ふじさきたつみさん、 他)

ＢＣの中点をＬ、ＡＢとＮＬの延長線の交点をＱとします。

参考図５

（２）までは解答例２と同様。

△ＮＢＣは二等辺三角形だから、ＮＱはＢＣの垂直二等分線。
よって、四角形ＢＬＮＰの３つの内角が直角なので、∠ＱＮＡも直角。

よって、△ＡＱＮ、△ＢＱＬもともに３：４：５の直角三角形。
従って、ＡＱ＝ＡＮ×５/３＝５×５/３＝２５/３ｃｍ。
ＢＱ＝ＡＱ−ＡＢ＝２５/３−６＝７/３ｃｍ。

ＢＬ＝ＢＱ×３/５＝７/３×３/５＝１．４ｃｍ。
従って、ＢＣ＝２×ＢＬ＝２×１．４＝２．８ｃｍ。

６．解答例５(有無相生さん、 他)

参考図６

途中までは解答例１などと同様。

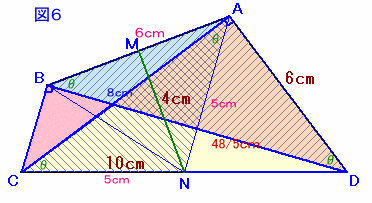
∠ＮＡＣ＝∠ＮＣＡ＝∠ＡＢＤ＝∠ＡＤＢ＝θより、
△ＮＡＣ∽△ＡＢＤで相似比は、ＮＡ：ＡＢ＝５：６。

よって、ＢＤ＝ＡＣ×６/５＝８×６/５＝４８/５ｃｍ。
従って、三平方の定理より、ＢＣ＝√（１０2−(48/5)2)＝２．８ｃｍ。

（その他の解法）