第２６６問の解答

---

１．問題　［平面図形］

左図のように、円状に並べられた５個の石があったとき、それぞれの石と「２つとなりの石」を線で結ぶと、それぞれの石にできる角度の和（図の赤い部分の角度の和）が１８０度になることはよく知られていますね。 では、円状に並べる石を１９個にして、それぞれの石と「７つとなりの石」を線で結ぶとすると、それぞれの石にできる角度の和は何度になるでしょうか。

---

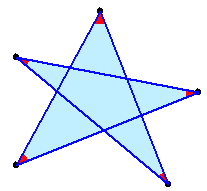２．解答例１(taroさん、長野美光さん、ＰＯＩさん、ＡЯＯＴさん、トトロ＠Ｎさん、あんみつさん、CRYING DOLPHINさん、a_pepperさん、有無相生さん、ハラギャーテイさん、他)

１９個の石が円周上に等間隔で並んでいるものと仮定します。

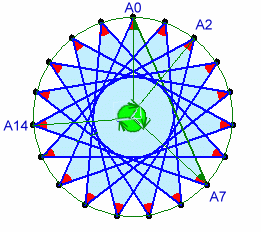
図１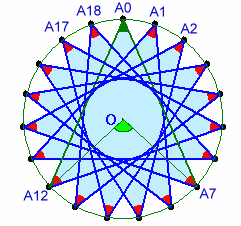

図２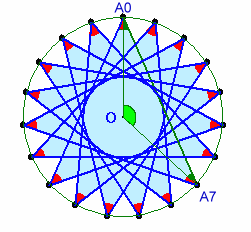

図１のように、円周角で考えると、
　∠A₁₂A₀A₇＝∠A₁₂OA₇×1/2＝360×(19-7×2)/19×1/2＝180×5/19

どの点でも内角は等しいので、求める和は、
　180×5/19×19＝900度
となります。

図２のように、二等辺三角形で考えると、
　∠A₁₂A₀A₇＝∠OA₀A₇＋∠OA₇A₀＝∠OA₀A₇＋∠OA₇A₀
＝180−∠A₀OA₇＝180−360×7/19

よって、求める和は、（180−360×7/19）×19＝180×19−360×7＝900度となります。

答：900度

以上

---

３．解答例２(ＡЯＯＴさん、中村明海さん、高橋道広さん、M.Hossieさん、澪桜葵美翔さん、航介さん、他)

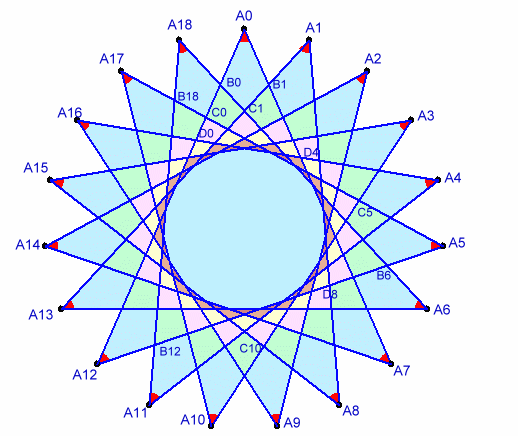
等間隔でないときでも、例えば図３で考えると、各点は、　A₀→A₇→A₁₄→A₂(≡21)→・・→A₀(≡7×19)
のように７周するので、内側の角度の和は、360度×7。

よって、求める和は、
Σ（180−内側の角）＝180×19−Σ（内側の角）＝180×19−360×7＝900度となります。

---

４．解答例３(鉄老さん、まるケンさん、他)

石がｎ個あるとします。

一つおきの石を結ぶとき、内角の和は、180度×(ｎ-2)、
２つおきだと、180度×(ｎ-2×2)、
・・・
m個おきだと、180度×(ｎ-ｍ×2)　となります。

本問では、ｎ＝19、ｍ＝７なので、180度×(19-7×2)＝９００度　となります。

---