第２６７問の解答

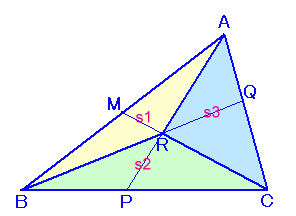
１．問題　［平面図形］

問題図
左図のような三角形ＡＢＣがあります。

いま、ＡＢの中点Ｍと辺ＡＣを３：４の比に分ける点Ｑをとり、ＣＭとＢＱの交点をＲとすると、ＡＲ＝ＣＲ＝４cm、ＢＲ＝５cmとなりました。

このとき、三角形ＡＢＣの面積を求めてください。

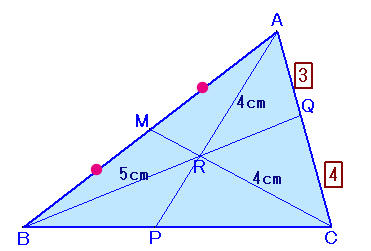２．解答例１(うっしーさん、CRYING DOLPHINさん、宮本会長さん、まるケンさん、あやのりんさん、Parpunteさん、ＫＩＮさん、トトロ＠Ｎさん、他)

まずCR:RM等の比を求める必要があります。
ここでは、チェバの定理、および下記の補題を用いてみましょう。

（チェバの定理）
Rを三角形の内部の点とし、ARの延長と辺BCの交点をP、ARの延長と
辺BCの交点をP、BQの延長と辺CAの交点をQ、CRの延長と辺ABの
交点をMとすろと、次式が成り立つ。

　参考図１
(AM/MB)・(BP/PC)・(CQ/QA)＝１

（証明）
s1＝△ABR、s2＝△BCR、s3＝△CARとします。
△ABP：△APC＝△RBP：△RPC＝BP：PC。
よって、s1：s3＝(△ABP−△RBP)：(△APC−△RPC)＝BP：PC。
　　・・・　（１）

同様に、
　s2：s1＝CQ：QA ・・・　（２）、　s3：s2＝AM：MB ・・・　（３）

（３）×（１）×（２）より、
　(AM/MB)・(BP/PC)・(CQ/QA)＝(s3/s2)・(s3/s2)・(s3/s2)＝１

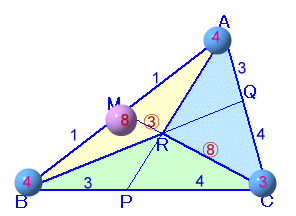
 （補題）
左図で、次式が成り立つ。
　AR/RP＝QA/CQ＋AM/MB、
　BR/RQ＝MB/AM＋BP/PC、
　CR/RM＝PC/BP＋CQ/QA

（証明）
　AR/RP＝△ABR/△RBP＝s1/(s2×BP/BC)、
　AR/RP＝△ARC/△RPC＝s3/(s2×PC/BC)。

よって、
　(AR/RP)×(BP/BC)＋(AR/RP)×(PC/BC)
　　＝s1/s2＋s3/s2
従って、
　AR/RP
＝s1/s2＋s3/s2
＝QA/CQ＋AM/MB

他も同様。　

　

チェバの定理より、
　(AM/MB)・(BP/PC)・(CQ/QA)＝１
　(1/1)・(BP/PC)・(4/3)＝１
よって、BP：PC＝３：４。

従って補題より、CR/RM＝PC/BP＋CQ/QA＝４/３＋４/３＝８/３。
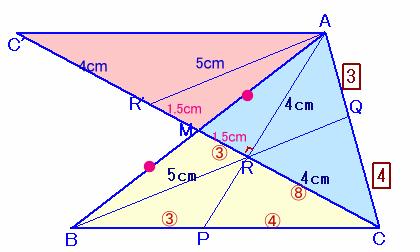
よって、RM＝CR×３/８＝４×３/８＝1.5cmとなります。

あるいは、補題を下図のようにおもり法で用いるとわかりやすいでしょう。

参考図１−１

ここで、△CBMを１８０度回転して、辺BMを辺MAに合わせてみます。

参考図２

△AR'M≡△ARMだから、AR'＝AR=５cm、R'M＝RM＝1.5cm、
よって、△AR'Rは辺の長さが３：４：５となり、直角三角形となります。

従って、△ABC＝△AC'C＝1/2×C'C×AR＝1/2×１１×４＝２２cm2となります。



　

答：２２ｃｍ2

以上

３．解答例２(マサルさん、takuさん、ヒデー王子さん、きょえぴさん、 他)

MR：RC＝３：８、MR＝1.5cmまでは解答例１と同様。

参考図３

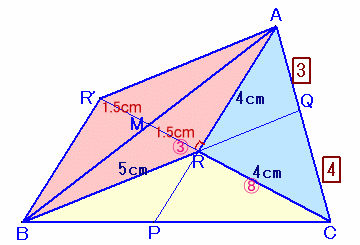
CMを延長して、ＭＲ'＝ＭＲとなるように、点Ｒ'をとります。
すると、△ＡＲ'Ｍと△ＡＲＭは、２辺挟角が等しいので合同。
従って、ＡＲ'＝ＢＲ＝５ｃｍ。
（同様に、BR'＝AR＝４ｃｍよりAR'BRは平行四辺形と分かります）

よって、△AR'Rは辺の長さが３：４：５となり直角三角形となります。
△AR'R＝1/2×３×４＝６cm2。

△ABC：△AR'R＝MR：MC＝３：１１、
よって、△ABC＝△AR'R×１１/３＝６×１１/３＝２２cm2。

(その他の解法)

MR：RC＝３：８等を求める方法として、

面積を求める方法として、

などがありました。