第268問の解答
1.問題 [速さの問題]
|
ある池の周りをマサルさんとトモエさんが逆方向に進みます。 2人は池のほとりのA地点から出発し、再びA地点で出会うまで池の周りをまわり続けます。すると2人は、最後にA地点で出会ったのを含めて、全部で11回すれ違ったそうです。 マサルさんの進む速さは時速6km、トモエさんの進む速さは時速△km(△は整数)であったそうです。 このとき、△に当てはまる整数として考えられるものを全て答えてください。 |
2.解答例1(CRYING DOLPHINさん、AЯOTさん、長野美光さん、BossFさん、高橋道広さん、澪桜葵美翔さん、巷の夢さん、 あんみつさん、ミミズクはくず耳さん、うっしーさん、幸せ配達人さん、Taroさん、H.Takaiさん、圭太さん、中村明海さん、DrKさん、まおさん、有無相生さん、M.Hossieさん、sodoさん、ちょこさん、トトロ@Nさん、他多数)
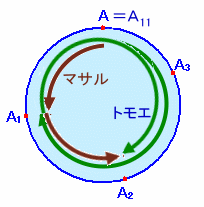
2人が最初に出会う点をA1、2回目に出会う点をA2、・・・とします。
また、池の周囲をd、およびAA1の距離(マサルさんが進む距離)と池の周囲との比をk(0<k<1)とおきます。
最初に出会うまでに2人で池を1周、2回目までに2周、・・・、11回目に出会うまでに11周します。
題意より、11回目に出会うのは元のA地点なので、マサルさんが池をn周(1≦n≦10)したとすると、トモエさんは(11−n)周します。
マサルさんはn周する間に11kd進むので、11kd=nd、
従ってk=n/11が成り立ちます。
すなわち、2人が出会う点は池を11等分した点となります。さて、2人の速度比は、n:(11−n)なので、
トモエさんの進む速さは、6×(11−n)/nとなります。これが整数となるのは、nが6の約数となるn=1、2、3、6のときで、
6×10/1=60、6×9/2=27、6×8/3=16、6×5/6=5kmとなります。答:5、16、27、60km
以上