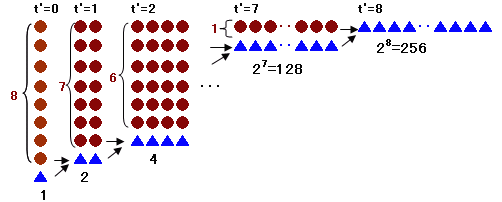第２６９問の解答

---

１．問題　［規則性の問題］

自己増殖型ロボットのフエール君とネオ・フエール君が１台ずつあります。 フエール君は、自分自身のコピーを１分間に１台作ります。 ネオ・フエール君は１分間に、１台のフエール君を壊し、それを材料にして１台のネオ・フエール君を作ります。 いま、１台のフエール君を空き地に置き、３分後にネオ・フエール君を１台、同じ空き地に置きました。するとその数分後、フエール君は１台もなくなってしまったそうです。 では、この数分間に壊されたフエール君は、全部で何台でしょうか。

---

２．解答例１(ミミズクはくず耳さん、あんみつさん、武田浩紀さん、ＡЯＯＴさん、トトロ＠Ｎさん、長野美光さん、takuさん、 澪桜葵美翔さん、有無相生さん、桜子さん、永井暁さん、DrKさん、ななしひめさん、sodoさん、チョコとプラスアルファさん、バーニィさん、 他多数)

t分後におけるフエール君の台数をF_t、ネオ・フエール君をN_tとします。

0≦t≦2では、フエール君だけなので、F_t+1=2F_tと等比級数になり、F₁=2、F₂=4、F₃=8、と順次計算できます。
また、ネオ・フエール君は、題意より、N₀=N₁=N₂=0、N₃=1となります。

さて、3≦tでは、題意より、
　N_t+1=2N_t　　　　・・・（１）
　F_t+1=2(F_t-N_t)　・・・（２）
が成り立ちますので、順次計算していけば下表のようになります。

フエール君が壊された台数分だけネオ・フエール君が増加するので、結局N₁₁-N₃=256-1=255台ということになります。

答：２５５台

以上

---

３．解答例２(長野美光さん、まるケンさん、宮本伸之さん、高橋道広さん、少年さん、M.Hossieさん、Parpunteさん、 他)

３分後以降のフエール君とネオ・フエール君の台数比を考えます。

ネオ・フエール君は１分ごとに同じ台数だけのフエール君を破壊して、２倍に増えていきます。従って、台数比は１ずつ減っていき、８分後に０となります。

このとき、ネオ・フエール君は２⁸＝２５６台になっているので、増加分の２５６−１＝２５５台に相当するフエール君を破壊したことになります。

---

（参考）漸化式で、一般式を考えてみましょう。(3分後をt=0とします）

　N_t+1=2N_t　　　　・・・（１）
　F_t+1=2(F_t-N_t)　・・・（２）

（２）÷（１）より、
　F_t+1/N_t+1=(F_t-N_t)/N_t
＝F_t/N_t−１

よって、F_t/N_tは１分ごとに１ずつ減っていくことになります。
　F_t/N_t＝8−t

また、（１）より、N_t＝２^t
従って、F_t＝（8−t）２^tとなります。

（別解）

あるいは、（２）より、
　F_t+2=2(F_t+1-N_t+1)　・・・（３）

（３）−（２）×２より、
　F_t+2-2F_t+1
=2F_t+1-4F_t-2N_t+1+4N_t　
=2F_t+1-4F_t

よって、
　F_t+2-4F_t+1+4F_t＝0　・・・（４）

（４）より、F_tは２階の線形漸化式となり、特性方程式はx²-4x+4=0なので、x=2を重根に持ちます。従って、一般式は、a、bを定数として、F_t＝（at+b）2^tと表すことができます。（注）

F₀=b=8、F₁=(a+b)×2=14より、a=-1、b=8を得ます。
よって、F_t＝（8−t）2^tとなります。

（注）
　G_t=F_t/2^tとおきます。すなわち、F_t＝2^tG_t
（４）に代入して、
　2^t+2G_t+2-4×2^t+1G_t+1+4×2^tG_t＝0　
　G_t+2-2G_t+1+G_t＝0
　G_t+2-G_t+1=G_t+1-G_t
従って、G_tは等差数列になり、a、bを定数として、G_t=at+bと表せます。
よって、F_t＝2^tG_t＝（at+b）2^tとなります。

---