第２７０問の解答

１．問題　［平面図形］

問題図
左図のような四角形ＡＢＣＤがあり、ＢＣ＝ＡＤ、∠ＡＤＣ＝６５度となっています。

いま、辺ＣＤの中点Ｍと辺ＡＢの中点Ｎを結ぶ直線と、直線ＣＢとの交点をＰとしたところ、∠ＭＰＣ＝２３度となりました。

このとき、∠ＢＣＤの大きさは何度でしょうか。

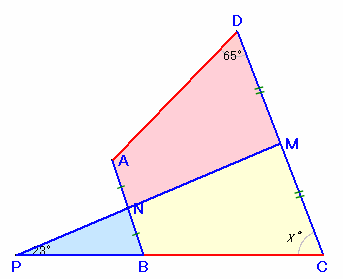２．解答例１(CRYING DOLPHINさん、M.Hossieさん、 他)

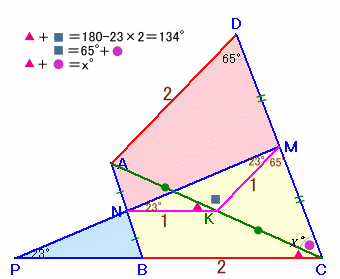
ACの中点をKとします。

参考図１

中点連結定理より、辺NKは辺BCに平行で、NK=BC×1/2。
同様に、辺MKは辺ADに平行で、MK=AD×1/2。

従って、AD=BCより、NK=MK。
よって、△KMNは二等辺三角形となります。

ここで、NKとPCが平行より、∠MNK＝∠NPB＝２３度、
∠NMK＝∠MNK＝２３度、∠AKN=∠ACB。
よって、∠NKM＝１８０−２３×２＝１３４度。

また、ADとKMが平行より、∠KMC=∠ADC=６５度。
∠AKMは△MKCの外角より、
∠AKM＝∠KMC＋∠MCK＝６５度＋∠MCK。

従って、１３４度−∠ACB＝６５度＋∠MCK。
よって、∠BCD＝∠ACB＋∠MCK＝１３４−６５＝６９度となります。

答：６９度

以上

３．解答例２(Michaelさん、ふじさきたつみさん、高橋道広さん、長野美光さん、 他)

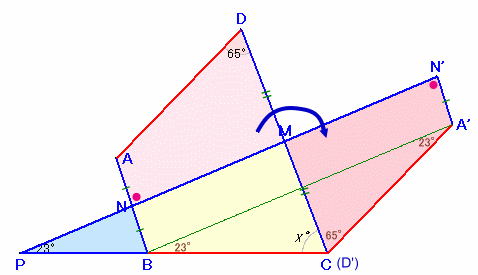
四角形DANMを点Mを中心に回転し、辺DMを辺CMに重ねたものを四角形CA'N'Mとします。

参考図２

∠CMN＋∠CMN'＝∠CMN＋∠DMN＝１８０度より、N、M、N'は一直線上に並びます。
∠ANM＝∠A'N'Mより、ANとA'N'は平行。
また、NB＝AN＝A'N'より、四角形NBA'N'は平行四辺形となり、
PN'とBA'も平行となります。

よって、∠A'BC＝∠MPC=２３度。

BC＝AD＝A'Cより、△CA'Bは二等辺三角形、
よって、∠BA'C＝∠A'BC＝２３度。

また、∠A'CM＝∠ADM＝６５度、
よって、△A'BCの内角の和を計算すると、
　∠BCD＋６５＋２３＋２３＝１８０度、
従って、∠BCD＝１８０−１１１＝６９度となります。

４．解答例３(有無相生さん、 他)

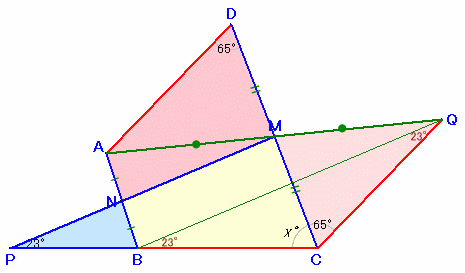
点CからADに平行な直線上に、CQ＝ADとなるよう点Qをとります。

参考図３

ADとCQが平行より、∠QCM＝∠ADM＝６５度。
また、AD＝CQ、DM＝CM。
従って、２辺と挟角が等しいので、△ADM≡△QCM。
よって、AM＝QM。

また、∠AMD＝∠CMQより、A、M、Qは一直線上に並びます。

△ABQでAN＝NB、AM＝MQだから中点連結定理より、PMとBQは平行。
よって、∠QBC＝∠MPC＝２３度。

また、BC＝AD＝CQより、△CQBは二等辺三角形、
よって、∠CQB＝∠QBC＝２３度。

従って、∠BCD＝１８０−（６５＋２３×２）＝６９度となります。