第271問の解答
1.問題 [場合の数]
|
マサルさんとツヨシ君がベーゴマ遊びをしています。 2人はともに3個のベーゴマを持って勝負をはじめました。 互いに手持ちのベーゴマの中から1個を使って勝負をし、 勝ったほうは相手のベーゴマをもらうことができます。 (引き分けはありません) その結果、11試合目でマサルさんの手持ちのベーゴマ3個が全てなくなり、 勝負はツヨシ君の勝利で終わりました。 では、この2人の勝負の星取表として考えられるものは何通りあるでしょうか。 |
2.解答例1(ミミズクはくず耳さん、ちーくん、AЯOTさん、トトロ@Nさん、武田浩紀さん、高橋道広さん、小西孝一さん、 他多数)
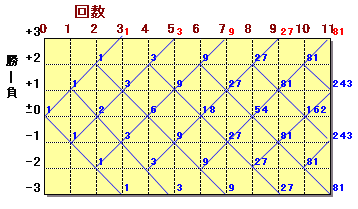
下図のような経路図を用いて計算します。
まず最初の地点を1とします。
次に、各交差点では、そこに至る交差点の数字を加えていきます。
11回目で勝負が決まるのは81通りあることになります。答:81通り
以上
3.解答例2(有無相生さん、 他)
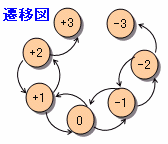
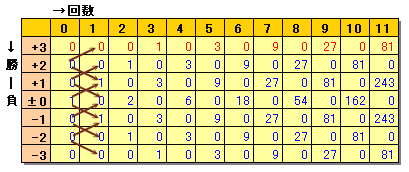
1回ごとに勝−負の状態を遷移図をもとに、下表のように計算します。
t回目の勝−負=nのときの場合の数を、P(n,t)とおきます。
t=0では、P(0,0)=1、P(n,0)=0(n≠0)
t>1では、
P(3,t+1)=P(2,t) ・・・(1)
P(2,t+1)=P(1,t) ・・・(2)
P(1,t+1)=P(2,t)+P(0,t) ・・・(3)
P(0,t+1)=P(1,t)+P(-1,t) ・・・(4)
P(-1,t+1)=P(0,t)+P(-2,t) ・・・(5)
P(-2,t+1)=P(-1,t) ・・・(6)
P(-3,t+1)=P(-2,t) ・・・(7)
が成り立つ。順次計算していけば、P(3,11)=81を得るので題意を満たすのは81通りとなり、ます。
4.解答例3(数楽者さん、ヒデー王子さん、 うっしーさん、kozzyさん、他)
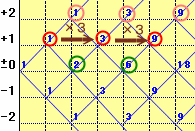
解答例1,2で容易に気がつくことは、
tが偶数のとき:P(3,t)=0
tが奇数のとき:P(3,t+2)=P(3,t)×3 (t≧3)・・・(ア)
となることです。
これより、P(3,2m+1)=3m(m≧0)と表せますので、P(3,11)=34=81通りとなります。[(ア)の証明]
まず、対称性より、P(-n,t)=P(n,t)が成り立ちますのでn≧0について考えれば十分です。
また、解答例2の(1)、(2)より、P(3,n+2)=P(2,n+1)=P(1,n)となるので、
n=1についての一般式を得れば良いことになります。(2)より、
P(2,2m)=P(1,2m-1) (m≧1)
(4)より、
P(0,2m)=P(1,2m-1)+P(-1,2m-1)=P(1,2m-1)×2
(3)より、
P(1,2m+1)=P(2,2m)+P(0,2m)=P(1,2m-1)+P(1,2m-1)×2
=P(1,2m-1)×3よって、P(3,2m+3)=P(3,2m+1)となり、(ア)が成り立ちます。
(その他の解法)
・樹形図等を用いて数え上げる・・・
あんみつさん、菊地翔伍さん、BossFさん、英理 さん、M.Hossieさん、チョコとプラスアルファさん、GENIUSさん、大岡敏幸さん、他