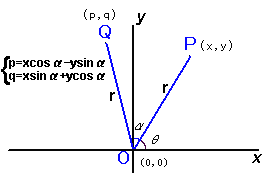第２７２問の解答

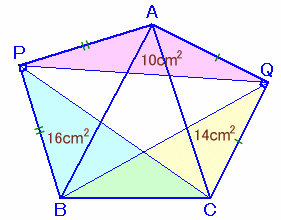
問題　［平面図形］

問題図
左図のような△ＡＢＣがあります。

いま、辺ＡＢ、辺ＡＣを斜辺とする直角二等辺三角形ＡＰＢ、ＡＱＣを図のように作ったところ、△ＡＰＱの面積が１０cm2、△ＢＣＰの面積が１６cm2、△ＢＣＱの面積が１４cm2となりました。

このとき、
（１）五角形ＡＰＢＣＱの面積は何cm2でしょうか？

（２）ＰＱの長さは何cmでしょうか？

　

解答例１(ヒデー王子さん、永井暁さん、他)

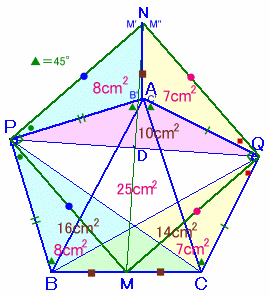
辺BCの中点をM、およびPQの中点をDとします。
△PBMを点Pを中心に回転し辺PBをPAに重ねたものを△PB'M'とし、△QCMを点Qを中心に回転し辺QCをQAに重ねたものを△QC'M''とします。

参考図１

　∠PAM'＋∠QAM''＋∠APQ
＝∠PBM＋∠QCM＋∠APQ
＝（∠ABC＋４５度）＋（∠ACB＋４５度）＋（４５度＋∠BAC＋４５度）
＝（∠ABC＋∠ACB＋∠BAC）＋１８０度
＝３６０度　
より、A、M'、M''は一直線上に並び、しかもAM'＝AM''（＝BC）だから、
M'とM''は一致します。・・・（１）
これを改めてNと呼ぶことにします。

PM＝PNで、∠MPN＝∠MPA＋∠APN＝∠MPA＋∠BPM＝９０度より、
△PMNは、直角二等辺三角形。
同様に、△QMNも直角二等辺三角形。

従って、四角形NPMQは正方形となります。

さて、△ANP＝△BMP＝1/2×△BCP＝８cm2、
　　△ANQ＝△CMQ＝1/2×△BCQ＝７cm2、
よって、△PNQ＝△ANP＋△ANQ＋△APQ＝８＋７＋１０＝２５cm2。

△PNQの面積は、PDを一辺とする正方形の面積に等しいので、
PD＝５ｃｍ、よって、PQ＝１０cmと分かります。　

また、△PMQ＝△PNQ＝２５cm2。
よって、五角形APBCQ
＝△APQ＋△BMP＋△CMQ＋△PMQ
＝１０＋８＋７＋２５＝５０cm2　となります。

答：（１）１０cm　（２）５０cm2

以上

解答例２(CRYING DOLPHINさん、他)

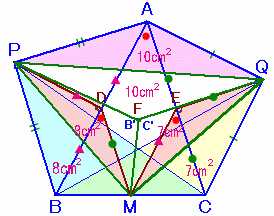
辺BCの中点をM、辺ABの中点をD、およびACの中点をEとします。

参考図２

中点連結定理より、DM＝1/2×AC＝EQ。
同様に、EM＝1/2×AB＝DP。
また、∠PDM＝９０度＋∠BDM＝９０度＋∠MEC＝∠MEQ。

従って、△DPMと△EMQは、２辺と挟角が等しいので合同。
よって、PM＝QM。

次に、PMを軸として△PBMを折り返したものを△PB'M、
QMを軸として△QCMを折り返したものを△QC'Mとします。

解答例１の（１）と同様にして、B'とC'は一致します。
これを改めてFと呼ぶことにすると、
FP＝BP＝AP、FQ＝CQ＝AQ。
よって、三辺が等しいことから△FPQ≡△APQ。

よって、五角形APBCQ
＝（△APQ＋△BMP＋△CMQ）×２
＝（１０＋８＋７）×２＝５０cm2　となります。

さて、∠FMP＝∠BMP、∠FMQ＝∠CMQより、
（∠FMP＋∠FMQ）×２＝∠BMC＝１８０度、
よって、∠FMP＋∠FMQ＝９０度。

従って、△PMQは直角二等辺三角形となります。
△PMQ＝１０＋８＋７＝２５cm2　となるので、PQ＝１０ｃｍとなります。

解答例３(マサルさん、武田浩紀さん、 名倉っちさん、ふじさきたつみさん、他)

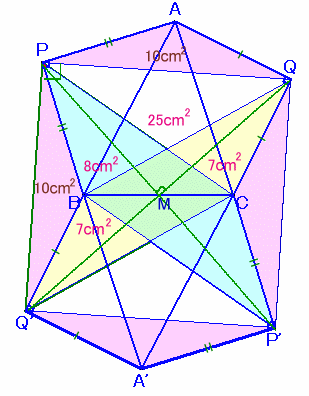
五角形APBCQを辺BCの中点Mを中心に１８０度回転したものを、A'P'CBQ'とします。

参考図３

　∠PBQ
＝３６０度−（∠PBC＋∠Q'BC）
＝３６０度−（∠PBC＋∠QCB）
＝３６０度−（∠ABC＋４５度＋∠ACB＋４５度）
＝９０度＋１８０度−（∠ABC＋∠ACB）
＝９０度＋∠BAC
＝∠PAQ。

よって、△APQと△B'PQ'は、２辺と挟角が等しいので合同。
従って、PQ'＝PQ。

また、∠QPQ'＝∠BPQ'＋∠QPB＝∠APQ＋∠QPB＝９０度。
従って、△PQ'Qは直角二等辺三角形となります。
また、MはQQ'の中点だから△MPQ'も直角二等辺三角形となります。

△BPQ'＝△APQ＝１０cm2、
△PBM＝1/2×△PBC＝８cm2、
△Q'BM＝1/2×△Q'BC＝1/2×△QBC＝7cm2。

よって、△MPQ'＝１０＋８＋７＝２５cm2。
これは、PQ'の半分の長さを１辺とする正方形の面積に等しいことから、
1/2×PQ'＝５cm。
従って、PQ＝PQ'＝１０cmとなります。

また、△MPQも△MPQ'と合同な直角二等辺三角形となるので、
△MPQ＝２５cm2。

よって、五角形APBCQ
＝△APQ＋△BMP＋△CMQ＋△MPQ
＝１０＋1/2×１６＋1/2×１４＋２５＝５０cm2　となります。

解答例４(ミミズクはくず耳さん、N.Nishiさん、他)

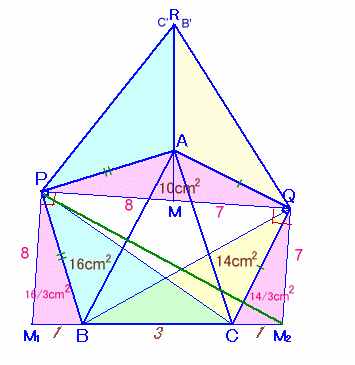
点Pを中心に△PBCを回転し、PBがPAに重なるようにしたものを△PAC'、
点Qを中心に△QCBを回転し、QCがQAに重なるようにしたものを△QAB'とします。

参考図４

解答例１の（１）と同様にして、C'とB'は一致しますので、これを改めてRとおきます。RAを延長し、PQとの交点をMとします。

点Pを中心に△APMを回転し、PAがPBに重なるようにしたものを△BPM1、
点Qを中心に△AQMを回転し、QAがQCに重なるようにしたものを△CQM2
とします。

∠PBM１＋∠PBC＝∠PAM＋∠PAR＝１８０度、
∠QCM2＋∠QCB＝∠QAM＋∠QAR＝１８０度より、
M1、B、C、M2は、一直線上に並びます。

また、∠M１PQ＝∠BPM１＋∠BPQ＝∠APM＋∠BPQ＝９０度、
同様に∠PQM2＝９０度となります。
また、PM1＋QM2＝PM＋QM＝PQ。
従って、四角形PM1M2Qは、面積がPQを１辺とする正方形のちょうど半分となる台形になります。

△BPM１と△CQM2は、底辺の長さが等しいので、面積の比は高さの比に等しい。よって、△BPM１：△CQM2＝△PBC：△QCB＝８：７。

また、△APMと△AQMは高さが共通なので、面積比は底辺の比に等しい。
よって、PM：QM＝△APM：△AQM＝△BPM１：△CQM2＝８：７。

従って、△BPM１＝△APM＝△APQ×8/15＝16/3cm2、
△CQM2＝△AQM＝△APQ×7/15＝14/3cm2となります。

よって、M1B：BC＝△BPM１：△PBC＝１：３、
　　M2C：BC＝△CQM2：△QBC＝１：３、
従って、M1B：BC：M2C＝１：３：１となります。

すると、△PM1M2＝△PBC×5/3＝80/3cm2。
△PQM2と△PM1M2の高さはPQと共通なので、
△PQM2＝△PM1M2×7/8＝70/3cm2。
よって、台形PM1M2Q＝△PM1M2＋△PQM2＝80/3＋70/3＝50cm2。

△PQM＝△BPM１＋△CQM2より、
五角形APBCQ＝台形PM1M2Q＝50cm2。

よって、PQを１辺とする正方形の面積は、５０×２＝１００cm2、
PQ＝１０ｃｍとなります。

解答例５(うっしーさん、 他)

点Qを中心に△APQを回転し、APがCQに重なるようにしたものを△QCP'、
△PBCを180度回転し、BCがCBに重なるようにしたものを△P''CBとします。

参考図５

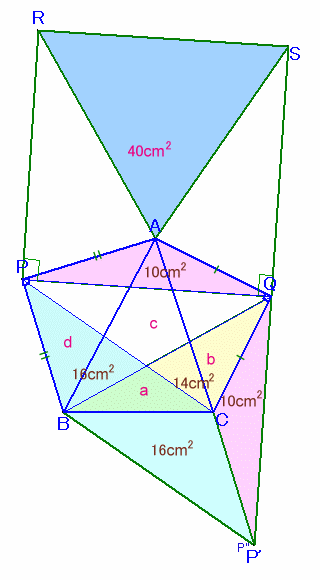
これまで同様にP''はP'と一致します。
よって、△QBP'＝１４＋１６＋１０＝４０cm2。

点Pを中心に△QPBを回転し、PBがPAに重なるようにしたものを△PAR、
点Qを中心に△PCQを回転し、QCがQAに重なるようにしたものを△SAQとします 。

PR＝PS＝PQ。
∠RPQ＝∠RPA＋∠APQ＝∠QPB＋∠APQ＝９０度、
同様に、∠PQS＝９０度、
従って、四角形RPQSは正方形となります。

また、△RASと△QBP'は三辺が等しいので合同、
△RAS＝△QBP'＝４０cm2。

従って、△RAS＋△APQ＝正方形RPQS×1/2＝５０cm2。
よって、正方形RPQS＝１００cm2となるので、正方形の１辺PQ＝１０ｃｍと分かります。

四角形PBCQを４つの三角形に分割し、面積をそれぞれａ、ｂ、ｃ、ｄとします。
　△ＱＢＣ＝ａ＋ｂ＝１４　・・・（１）
　△ＰＢＣ＝ａ＋ｄ＝１６　・・・（２）
　△ＲＰＡ＋△ＳＡＱ＝（ｃ＋ｄ）＋（ｃ＋ｂ）
　　＝正方形ＲＰＱＳ−（△RAS＋△APQ）＝５０　・・・（３）

（３）−（１）−（２）より、
　（２ｃ＋ｂ＋ｄ）−（ａ＋ｂ）−（ａ＋ｄ）＝５０−３０
よって、ｃ−ａ＝１０。　・・・（４）

（４）を（１）に代入して、
　（ｃ−１０）＋ｂ＝１４
よって、ｂ＋ｃ＝２４となります。

従って、五角形APBCQ
＝１０＋ａ＋ｂ＋ｃ＋ｄ
＝１０＋（ａ＋ｄ）＋（ｂ＋ｃ）
＝１０＋１６＋２４
＝50cm2。

解答例６(トトロ＠Nさん、他)

点Ｒを辺ＱＡの延長線上に、点Ｔを辺ＱＣの延長線上に、および点Ｓを四角形ＲＳＴＱが長方形になるようにとります。

参考６

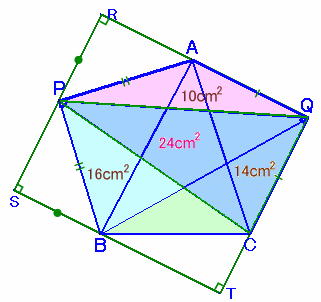
△ＲＰＡと△ＳＢＰは、ＰＡ＝ＢＰ、∠ＰＡＲ＝９０−∠ＢＰＳ＝∠ＢＰＳ、および∠ＲＰＡ＝９０−∠ＢＰＳ＝∠ＳＢＰより、１辺と２挟角が等しいので合同。
よって、ＲＰ＝ＳＢ。

従って、△ＡＰＱ＋△ＱＢＣ
＝1/2×ＡＱ×ＲＰ＋1/2×ＱＣ×ＢＴ
＝1/2×ＱＣ×ＳＢ＋1/2×ＱＣ×ＢＴ
＝1/2×ＱＣ×（ＳＢ＋ＢＴ）
＝△ＱＰＣ
よって、△ＱＰＣ＝△ＡＰＱ＋△ＱＢＣ＝１０＋１４＝２４ｃｍ2。

従って、五角形ＡＰＢＣＱ
＝△ＡＰＱ＋△ＱＰＣ＋△ＰＢＣ
＝１０＋２４＋１６＝５０ｃｍ2。

ＰＱの長さは、省略。

解答例７(川田智之さん、 他)

解答例５と同様に点Ｐ'を取ります。また、ＰＣとＱＢの交点をＳとします。

参考７

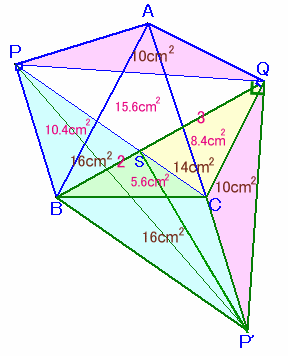
△ＱＰＰ'はＰＱ＝Ｐ'Ｑの直角二等辺三角形、およびＰＢＰ'Ｃは平行四辺形となります。

従って、△ＳＢＰ'＝△ＰＢＰ'＝1/2×ＰＢＰ'Ｃ＝１６ｃｍ2。
また、△ＱＳＰ'＝△ＱＢＰ'＝４０−１６＝２４ｃｍ2。
よって、ＢＳ：ＳＱ＝△ＳＢＰ'：△ＱＳＰ'＝２：３。

従って、△ＳＢＣ：△ＳＣＱ＝ＢＳ：ＳＱ＝２：３。
よって、△ＳＢＣ＝△ＱＢＣ×2/5＝１４×2/5＝５．６ｃｍ2、
　△ＳＣＱ＝△ＱＢＣ×3/5＝１４×3/5＝８．４ｃｍ2。
　△ＰＢＳ＝△ＰＢＣ−△ＳＢＣ＝１６−５．６＝１０．４ｃｍ2、
　△ＰＳＱ＝△ＰＢＳ×3/2＝１０．４×3/2＝１５．６ｃｍ2。

よって、五角形ＡＰＢＣＱ
＝１０＋１０．４＋１５．６＋５．６＋８．４＝５０ｃｍ2。

また、△ＱＰＰ'＝△ＰＢＱ＋△ＱＢＰ'−△PBP'＝２６＋４０−１６＝５０ｃｍ2。
△ＱＰＰ'は直角二等辺三角形なので、PQ＝１０ｃｍと分かります。

（その他の解法）

・座標、三角関数等を用いて解く・・・
　Taroさん、有無相生さん、高橋道広さん、長野美光さん、電卓マニアさん、
　M.Hossieさん、sodoさん、ばつ丸さん、Parpunteさん、他

（解答例８）

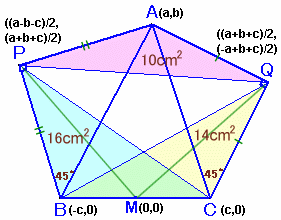
BCの中点Mを原点にとり、A（a,b）、B（-c,0）、C（c,0）とおきます。

参考図８ （参考図）
参考図９

　Px＝-c+((a+c)cos45°-bsin45°)/√2＝（a-b-c)/2
　Py＝　　((a+c)sin45°+bcos45°)/√2＝（a+b+c)/2
　Qx＝c+((a-c)cos(-45°)-bsin(-45°))/√2＝（a+b+c)/2
　Qy＝　　((a-c)sin(-45°)+bcos(-45°))/√2＝（-a+b+c)/2

従って、△PBC＝ｃPy＝ｃ(a+b+c)/2＝16、
よって、a+b+c＝32/c ・・・（１）　
また、△QBC＝ｃQy＝ｃ(-a+b+c)/2＝14、
よって、-a+b+c＝28/c ・・・（２）　

（１）−（２）より、　2a＝4/c、
よって、a＝2/c。　・・・（３）
（１）＋（２）より、　2(b+c)＝60/c、
よって、b＝30/c-c。　・・・（４）

∠ABC=α、∠ACB＝β、∠BAC＝γとおきます。

また、△APQ
＝1/2×AP×AQ×sin(γ＋９０°)
＝1/2×AB/√2×AC/√2×cos(γ)
＝1/4×AB×AC×cos(180°-α-β)
＝−1/4×AB×AC×cos(α+β)
＝−1/4×AB×AC×{cosαcosβ-sinαsinβ}
＝−1/4×{ABcosαACcosβ-ABsinαACsinβ}
＝−1/4×{(a+c)(c-a)-b2}
＝1/4×(a2+b2-c2)＝10
よって、a2+b2-c2＝40。　・・・（５）

（３）、（４）を（５）に代入して、
　(2/c)2＋(30/c-c)2-c2＝40、
　c2＝9.04、
よって、c＝√9.04≒3.01cm。
従って、（３）、（４）より、
　a＝2/√9.04≒0.67cm、b＝30/√9.04-√9.04≒6.97cm。

さて、△PMQが直角二等辺三角形であることが次のようにして分かります。
まず、Qｘ＝Pｙ＝（a+b+c)/2、Qｙ＝−Pｘ＝（-a+b+c)/2より、
（Py/Px）・（Qy/Qx)＝（Py/Px）・（−Pｘ/Pｙ)＝−１より、PMとQMは直交します。
そして、QM2＝Qx2＋Qｙ2＝Py2＋Px2＝PM2より、PM＝QM。
実際に計算すると、
PM2＝｛（-a+b+c)/2｝2＋｛（a+b+c)/2｝2
　　＝｛a2+(b+c)2｝｝/2
　　＝｛(2/c)2+(30/c)2｝/2
　　＝(904/c2)/2
　　＝100/2＝50
よって、PM＝QM＝5√2。
PQ＝√2×PM＝√2×5√2＝１０ｃｍ。

従って、△MPQ＝1/2×PM2＝２５cm2。
よって、五角形APBCQ
＝△APQ＋△BMP＋△CMQ＋△MPQ
＝１０＋1/2×１６＋1/2×１４＋２５＝５０cm2　となります。