第273問の解答
問題 [整数の性質]
|
ある2ケタの整数があります。この整数は、奇数であることが分かっています。 いま、この2ケタの整数に1〜9までのどの整数をかけても、各位の数の和は、もとの2ケタの整数の各位の数の和と変わらなかったそうです。 では、もとの2ケタの整数として考えられるものをすべて答えてください。 |
解答例1(CRYING DOLPHINさん、永井暁さん、Taroさん、中川幸一さん、名倉っちさん、有無相生さん、DrKさん、川田智之さん、他)
もとの整数をn=q×10+r、
これをm倍したものをn×m=p'×100+q'×10+r'とします。n=q×9+(q+r)、n×m=p'×99+q'×9+(p'+q'+r')
と表せる。
従って、題意より、
n−q×9=n×m−(p'×99+q'×9)
n×(m−1)=p'×99+(q+q')×9 ・・・(1)1≦m≦9で(1)が成り立つことより、nは9の倍数でなければならない。
題意より、nは2桁の奇数であることから、候補となる整数は、
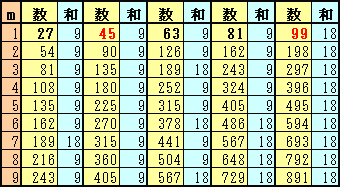
27、45、63、81、99に絞られます。これら5つの整数について、m倍した整数と、その各位の和を計算すると下表のようになります。
従って、題意を満たす整数は45と99の2通りとなります。
答:45、99
以上
その他(EXCELなどを用いて計算して求める)
まるケンさん、丸天後藤様、ちば けいすけさん、峰富士子さん、ぶるぼんさん、他