第２７４問の解答

問題　［平面図形］

問題図
左図のような△ＡＢＣがあります。

この三角形は、面積が９cm2、辺ＡＢ＝６cm、∠ＡＣＢ＝４５度となっています。また、∠ＢＡＣは９０度より大きいそうです。

このとき、∠ＡＢＣの大きさを求めてください。

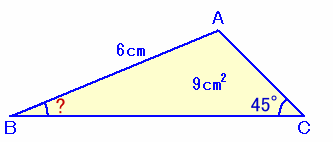解答例１(長野美光さん、あんみつさん、 まるケンさん、他)

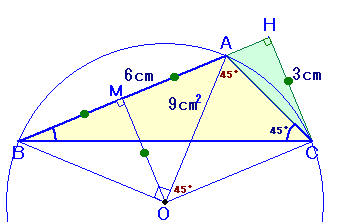
△ＡＢＣの外接円の中心をＯ、辺ＡＢの中点をＭ、点Ｃから辺ＡＢに下ろした垂線の足をＨとします。

参考図１

△ＡＢＣ＝1/2×ＡＢ×ＣＨ＝９ｃｍ2。
よって、CH＝９／ＡＢ×２＝９／６×２＝３ｃｍ。

弧ＡＢに対する中心角が∠ＡＯＢ、円周角が∠ＡＣＢなので、
∠ＡＯＢ＝∠ＡＣＢ×２＝４５×２＝９０度。
従って、△ＡＢＯはＡＯ＝ＢＯの直角二等辺三角形となります。
よって、ＯＭ＝ＡＭ＝ＢＭ＝1/2×ＡＢ＝３ｃｍ、∠ＢＡＯ＝∠ＡＢＯ＝４５度となります。

ＣＨとＯＭは、ともに辺ＡＢに対して垂直だから平行、しかも長さが等しいので、四角形ＭＯＣＨは長方形となります。
従って、ＡＢとＯＣは平行、よって∠ＡＯＣ＝∠ＢＡＯ＝４５度。

弧ＡＣに対する中心角が∠ＡＯＣ、円周角が∠ＡＢＣなので、
∠ＡＢＣ＝∠ＡＯＣ×1/2＝４５×1/2＝２２．５度となります。

答：２２．５度

以上

解答例２(CRYING DOLPHINさん、他)

∠ＡＢＣ＝２２．５度と仮定します。点Ａから辺ＢＣに下ろした垂線の足をＨとします。

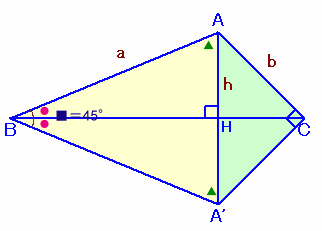
図１
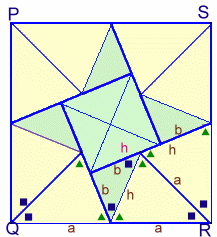
参考図２−１		 図２
参考図２−２

図１のように、△ＡＢＣを２つ合わせでできる△ＡＢＡ'と△ＡＣＡ'を８個ずつ使って、図２のように一辺の長さがａ×２の正方形の中に敷き詰めることができます。（ただし、ＡＢ＝ａ、ＡＣ＝ｃ、ＡＡ'＝ｈ）

従って、△ＡＢＣ×２×８＝(2a)2＝4a2、
よって、△ＡＢＣ＝1/4×a2＝1/4×６2＝９ｃｍ2。

これより、∠ＡＢＣ＝２２．５度とする△ＡＢＣは題意を満たします。

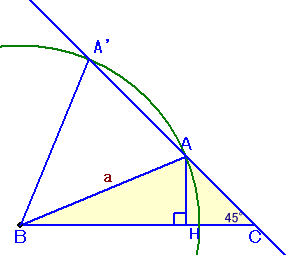
ところで、Ａは点Ｂを中心とする半径ａの円と、Ｃを通り辺ＢＣと４５度をなす直線の交点であるので、下図のように最大２個（Ａ、Ａ'とします）しか存在しない。
しかるに、∠ＢＡＣ＋∠ＢＡ'Ｃ＝１８０度なので、∠ＢＡＣが１８０度より大きいものは、このうち１個だけである。

参考図２−３

よって、∠ＡＢＣ＝２２．５度と結論づけることができる。

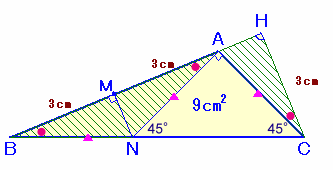
解答例３(ちば けいすけさん、takuさん、小西孝一さん、トトロ＠Ｎさん、鉄老さん、他)

辺ＢＣ上に∠ＣＡＮ＝９０度となるように点Ｎを取ります。
また、点ＣおよびＮから辺ＡＢに下ろした垂線の足をそれぞれＨ、およびＭとします。

参考図３

解答例１と同様に、△ＡＢＣ＝９ｃｍ2より、ＣＨ＝３ｃｍが得られます。

さて、∠ＡＮＣ＝１８０−（∠ＣＡＮ＋∠ＡＣＮ）＝１８０−（９０＋４５）＝４５度、よって、△ＡＮＣは直角二等辺三角形となります。
従って、ＡＮ＝ＡＣとなります。

△ＡＮＭと△ＣＡＨについて、ＡＮ＝ＡＣ、∠ＮＡＭ＝９０−∠ＣＡＨ＝∠ＡＣＨ、および∠ＡＮＭ＝９０−∠ＮＡＭ＝∠ＣＡＨ、
よって一辺とその両端の角が等しいので合同。
従って、ＡＭ＝ＣＨ＝３ｃｍ、ＢＭ＝ＡＢ−ＡＭ＝３ｃｍとなります。

△ＡＮＭと△ＢＮＭについて、ＢＭ＝ＡＭ＝３ｃｍ、ＭＮは共通、∠ＢＭＮ＝∠ＡＭＮ＝９０度、よって２辺挟角が等しいので合同。

これより、∠ＮＢＭ＝∠ＮＡＭとなります。
ところが、∠ＡＮＣは△ＮＢＡの外角より、
　∠ＮＢＭ＋∠ＮＡＭ＝∠ＡＮＣ、
　∠ＡＢＣ×２＝４５度、
よって∠ＡＢＣ＝２２．５度となります。

（参考）
結果として同じ図になりますが、点ＭをＡＢの中点、ＮをＡＢの垂直二等分線とＢＣの交点とした場合、△ＡＮＭ≡△ＢＮＭまではすぐ分かりますが、これらが△ＡＣＨと合同となることを示すのはかなり難しいようです。

従って、解答例２のように∠ＡＢＣ＝２２．５度と仮定して題意を満たすことを示し、しかも題意を満たす△ＡＢＣは一意的に定まることを用いると良いでしょう。

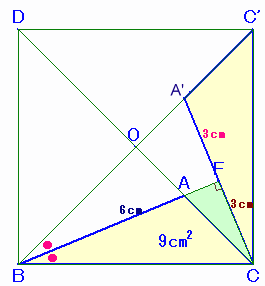
解答例４(ふじさきたつみさん、他)

辺BCを一辺とする正方形を考え、対角線の交点をOとします。

参考図４

△ABCを０を中心に反時計回りに９０度回転したものを△A'CC'とし、BAの延長とA'Cとの交点をFとします。

A'CはABが９０度回転したものだから両者は直交します。
従って、△ABC＝1/2×AB×CFより、CF＝３ｃｍとなります。

A'F＝A'C−CF＝６−３＝３ｃｍ。

よって、△BA'Fと△BCFについて、BA'＝BC、BFは共通、∠BA'F＝∠BFC＝９０度より、２辺挟角が等しいので合同。
従って、∠Ａ'ＢＦ＝∠ＣＢＦ（＝∠ＡＢＣ）。

よって、∠ＡＢＣ×２＝∠ＯＢＣ＝４５度、
従って、∠ＡＢＣ＝４５×1/2＝２２．５度となります。

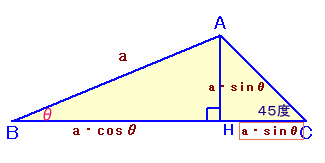
解答例５(うっしーさん、中川幸一さん、ハラギャーテイさん、高橋道広さん、M.Hossieさん、King of Kingさん、他)

参考図５

上図より、AB=aとおくと、
　ＡＨ＝CH＝a・sinθ、BH＝a・cosθ、
よって、
　△ABC＝1/2・（a・cosθ＋a・sinθ）・a・sinθ
　　＝1/2×a2・（cosθ＋sinθ）・sinθ
従って、
　1/2×６2・（cosθ＋sinθ）・sinθ＝９、
　２（cosθ＋sinθ）・sinθ＝１、
　２cosθ・sinθ＋２sin2θ＝１。

三角関数の倍角公式より、sin2θ＝２cosθ・sinθ、cos2θ＝１−２sin2θ、
よって、sin2θ＝cos2θ、従ってtan2θ＝１。
∠BAC＞１８０度より、θ＜４５度、よって、2θ＝４５度、
θ＝２２．５度となります。