第２７５問の解答

---

問題　［平面図形］

左図のような辺ＡＣ＝７cm、∠Ａ＝９０度の直角三角形ＡＢＣがあります。 いま、ＡＢ上のＢＤ＝４cmの位置に点Ｄ、ＡＣ上のＡＥ＝４cmの位置に点Ｅをとり、ＢＣの中点Ｍと結んだところ、∠ＤＭＥ＝９０度となりました。 このとき、△ＡＢＣの面積を求めてください。

---

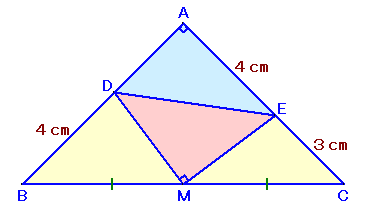解答例１(ふじさきたつみさん、ミミズクはくず耳さん、 小西孝一さん、takuさん、永井暁さん、Taroさん、高橋道広さん、他)

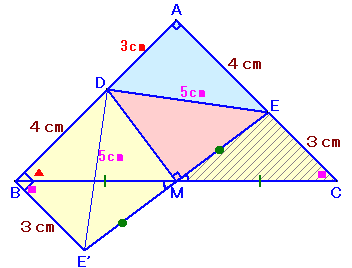
点Mを中心に△EMＣを180度回転し、CMをBMに重ねたものを△E'MＣとします。

∠EMC＝∠E'MCより、点E、M、E'は一直線上に並びます。
従って、∠DME'＝180度-∠DME＝90度。
よって、△DMEと△DME'は二辺挟角が等しいので合同。
従って、DE＝DE'となり、△DE'Eは二等辺三角形となります。

△ＡＢCは直角三角形だから、∠ABC＋∠ACB＝90度。
よって、∠ABE'＝∠ABC＋∠CBE'＝∠ABC＋∠ACB＝90度。
よって、△DBE'は辺の長さが3：4：5の直角三角形となります。

従って、DE'＝DE=5cm。
すると、△ADEも辺の長さが3：4：5の直角三角形となり、AD＝3cmとなります。

従って、AB＝3+4＝7cm＝ACとなり、△ABCは直角二等辺三角形となります。よって、△ABC＝1/2×7²＝24.5cm²となります。

答：２４．５cm²

以上

　

（別解）
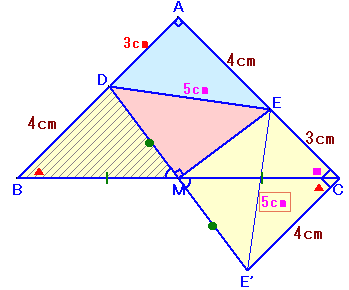
上記解法は、△EMCを回転しましたが、下図のように△DBMを回転しても同様に解けます。

また、DMまたはMEを軸に△DMEを折り返した場合も、ほぼ上記解法と同様になります。

---

解答例２(まるケンさん、他)

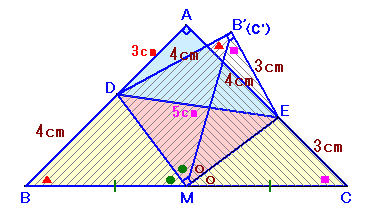
DMを軸に△DBMを折り返したものを△DB'M、およびMEを軸に△EMCを折り返したものを△EMC'とします。

∠DMB'＋∠EMC'＝∠DMB＋∠EMC＝90度＝∠DME、
よって、辺B'MとC'Mは重なります。
しかも、B'M＝BM＝MC＝C'Mより、B'とC'は一致します。

すると、∠DB'E＝∠DB'M＋∠MB'E＝∠DBM＋∠MCE＝90度、
また、DB'＝DB＝4cm、B'E＝EC＝3cm、
よって、△DB'Eは辺の長さが3：4：5の直角三角形となります。

従って、DE＝5cmとなり、△ADEも辺の長さが3：4：5の直角三角形。

以下、解答例１と同様にして、△ABC＝24.5cm²を得ます。

　

---

解答例３(M.Hossieさん、有無相生さん、アークさん、 他)

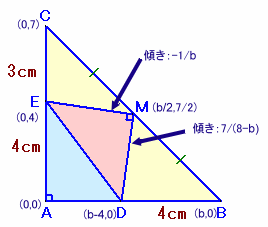
点Aを原点に取り、辺AB上をX軸に、辺ACをY軸にした座標系で考えます。
また、辺ABの長さをｂcmとおきます。

各点の座標は上図のようになるので、
直線MDの傾きは、（7/2）/（ｂ/2-（ｂ-4））＝7/（8-ｂ）、
直線EMの傾きは、（7/2-4）/（ｂ/2）＝-1/ｂ。

MDとEMは直交するので、傾きの積は-1、
従って、7/（8-ｂ）×（-1/ｂ）＝-1。

これより、ｂ（ｂ-8）+7＝0、（ｂ-1）（ｂ-7）＝0、
よって、ｂ＝1cmまたは7cm。

ｂ＝1cmのときはｂ-4＜0となり、点DがAB上にないので不適、
よってｂ＝7cmとなります。

従って、△ABC＝1/2×7²＝24.5cm²となります。

---