第276問の解答
問題 [整数の性質]
|
マサルさんとトモエさんが次のような会話をしています。 マサル:「何か好きな3ケタの整数を思い浮かべてごらん。」 トモエ:「ん〜、OK、決まったよ」 マサル:「じゃあ、それらの数の、各ケタを入れかえてできる5種類の整数を全部たして ごらん。」 トモエ:「ん〜、電卓使って良い?(笑)ん〜と、1688ね。」 さて、「トモエさんが最初に思い浮かべた整数」はいくつだったのでしょうか? |
解答例1(Taroさん、ミミズクはくず耳さん、 長野美光さん、小杉原啓さん、トトロ@Nさん、CRYING DOLPHINさん、ふきゅさん、まおさん、あまれっとさん、中川幸一さん、有無相生さん、M.Hossieさん、高橋道広さん、みーちゃんぶちゅうさん、DrKさん、チョコとプラスアルスァさん、他)
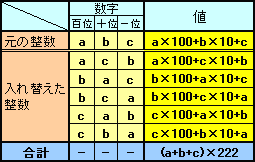
求める整数を、n=a×100+b×10+cとおきます。
各ケタを入れかえてできる5種類の整数は、
a×100+c×10+b
b×100+a×10+c
b×100+c×10+a
c×100+a×10+b
c×100+b×10+a
となります。ただし、題意より、0<a,b,c<10。従って、これらに元の整数を加えると、
2(a+b+c)×100+2(a+b+c)×10+2(a+b+c)=1688+n
(a+b+c)×222=7×222+134+n ・・・(1)
よって、n+134は222の倍数となります。m=a+b+c-7とおくと、(1)より、
m×222=n+134<1000+134=1134
従って、m+7<1134/222=5.1
よって、m≦3。
さて、
m=1のとき、n=222×1-134=88 不適
m=2のとき、n=222×2-134=310 不適
m=3のとき、n=222×3-134=532 適。
従って、n=532が求める整数と分かります。答:532
以上
解答例2(AЯOTさん、長野美光さん、N.Nishiさん、TEGさん、なみはやさん、他)
求める整数を、n=a×100+b×10+cとおきます。
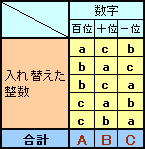
各ケタを入れかえてできる5種類の整数の、百位の数字を加えたものをA、十位の数字を加えたものをB、一位の数字を加えたものをCとします。
上図より、
a+2b+2c=A ・・・(1)
2a+ b+2c=B ・・・(2)
2a+2b+ c=C ・・・(3)
が成り立ちます。A-B=b-a、B-C=c-b、C-A=a-cより、A、B、Cの2個ずつの差は、9-1=8以内となります。
従って、入れ替えた整数の合計が1688となるには、繰り上がりを考慮すると、A=15、B=17、C=18以外には題意に適するものがありません。
よって、
a+2b+2c=15 ・・・(1)'
2a+ b+2c=17 ・・・(2)'
2a+2b+ c=18 ・・・(3)'
となります。(1)'+(2)'+(3)'より、
5(a+b+c)=50
よって、
a+b+c=10
2(a+b+c)=20 ・・・(4)(4)−(1)'より、a=20-15=5、
(4)−(2)'より、b=20-17=3、
(4)−(3)'より、c=20-18=2
を得ます。従って、求める整数は532となります。
解答例3(永井暁さん、圭太さん、かなさん、 ハラギャーテイさん、他)
求める整数を、n=a×100+b×10+cとおきます。
各ケタを入れかえてできる5種類の整数は、
a×100+c×10+b
b×100+a×10+c
b×100+c×10+a
c×100+a×10+b
c×100+b×10+a
となるので、合計すると、
a×122+b×212+c×221=1688 ・・・(1)
となります。(1)を変形して、
a×(221-99)+b×(221-9)+c×221=221×7+141
(a+b+c-7)×221=a×99+b+141 ・・・(2)
となります。p=a+b+c-7とおくと、(2)より、
a×99+b+141=p×221 ・・・(3)
となります。1≦a、b、c≦9より、-4≦p≦20、249=221+28≦a×99+b+141≦1113=221×5+8。
よって、(3)より、1≦p≦5の範囲に絞られます。 ・・・(4)さて、(3)を変形して、
(a×11+b+15)×9=p×24×9+p×5-6
p×5-6=(a×11+b+15-p×24)×9 ・・・(5)
が得られます。従って、p×5-6は9の倍数となり、(4)から-1≦p×5-6≦19、
よって、p×5-6=0、9、18のいずれかとなります。
これより、pが整数となるのは、p×5-6=9、p=3のときのみです。 ・・・(6)よって、(5)より、
a×11+b+15=73
a×11+b=58
(a-5)×11=3-b ・・・(7)
を得ます。-6≦3-b≦2なので、この範囲で11の倍数は0のみ。
従って、a-5=0、3-b=0、
よって、a=5、b=3となります。(6)より、a+b+c-7=3、従って、c=10-(a+b)=10-(5+3)=2となります。
以上から、求める整数は532と分かります。