第277問の解答
問題 [平面図形]
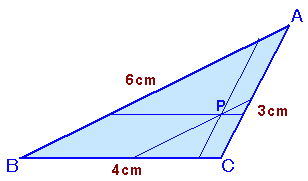 |
|
解答例1(まおさん、高橋道広さん、あまれっとさん、ちば けいすけさん、他)
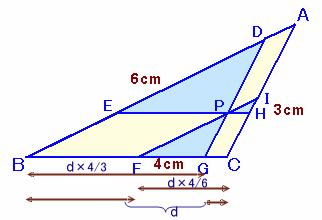
3本の直線(長さをdとする)と各辺の交点を下図のようにします。
題意より、△DBG、△IFC、△AEHおよび△DEP、△PFG、△IPHは△ABCと相似です。また、四角形ADPI、EBFP、PGCHは平行四辺形になります。
(このことは、他の解法でも共通に使います)従って、
BG:DG=BC:AC、よってBG=DG×BC/AC=d×4/3 ・・・(1)
FC:IF=BC:AB、よってFC=IF×BC/AB=d×4/6 ・・・(2)
BF+GC=EP+PH=d ・・・(3)(1)+(2)+(3)より、
BC×2=d×4/3+d×4/6+d=8
d×(1/3+1/6+1/4)=2
よって、d=2/(1/3+1/6+1/4)=8/3。答:8/3cm
以上
解答例2(ちーくん、H.Takaiさん、Parpunteさん、 他)
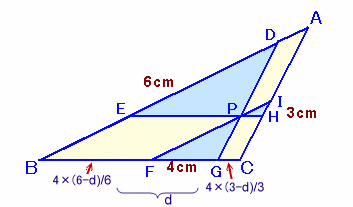
解答例1と同様にして、
FC=d×4/6、よってBF=4×(1−d/6)・・・(1)
BG=d×4/3、よってGC=4×(1−d/3)・・・(2)
FG=BC−EH=4−d・・・(3)(1)+(3)+(2)より、
FC+BG+FG=4×(1−d/6)+(4−d)+4×(1−d/3)
4=4×3−4×(1/6+1/4+1/3)×d
よって、d=2/(1/3+1/6+1/4)=8/3。
解答例3(AЯOTさん、exam_in_2004さん、ふじさきたつみさん、他)
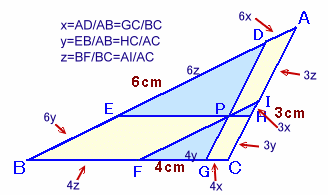
x=AD/AB=GC/BC、
y=EB/AB=HC/AC、
z=BF/BC=AI/ACとおきます。AD+EB=6x+6y=IP+PF=d ・・・(1)
HC+AI=3y+3z=PG+DP=d ・・・(2)
GC+BF=4x+4z=PH+EP=d ・・・(3)k=d/24とおきます。
(1)、(2)、(3)より、
x+y =4k・・・(4)
y+z=8k・・・(5)
x +z=6k・・・(6)(4)+(5)+(6)より、
2×(x+y+z)=18k
よって、
x+y+z=9k ・・・(7)さて、FG=PF×4/6=6y×4/6=4y
よって、GC+FG+BF=4×(x+y+z)=BC=4
従って、x+y+z=1・・・(8)(7)、(8)より、9k=1、k=1/9。
よって、d=24k=24×1/9=8/3。なお、x、y、zの値は、
(7)−(5)より、x=k=1/9、
(7)−(6)より、y=3k=3/9、
(7)−(4)より、z=5k=5/9
となります。
(その他の解法)
・相似比と方程式を使用する・・・
有無相生さん、M.Hossieさん、N.Nishiさん、小杉原啓さん、長野美光さん、POIさん、武田浩紀さん、トトロ@Nさん、CRYING DOLPHINさん、ヒデー王子さん、ミミズクはくず耳さん、巷の夢さん、DrKさん、ハラギャーテイさん、小西孝一さん、他