第278問の解答
問題 [確からしさ]
|
マサルさんはお祭りの夜店で、くじ引き屋さんの前でお店のおじさんと次のようなやりとりをしています。 マサル:「ルールは?」 おじさん:「Aの箱から1本、Bの箱から1本、それぞれくじをひいて、両方当たりなら1等ってわけさ。」 マサル:「両方当たる確率はどのくらいなの?」 おじさん:「えーい、ホントは秘密だけど教えちゃおう!ズバリ10分の1だよ。」 マサル:「じゃ、どっちか一方だけ当たる確率は?」 おじさん:「う〜ん、30分の17かな。高いだろう?」 マサル:「箱の中にくじは何本入ってるの?」 おじさん:「A、Bどっちも30本だよ。」 マサル:「AとB、当たりやすいのはどっち?」 おじさん:「Aだね!」 (1) 当たりくじはAの箱、Bの箱合わせて何本入っているでしょう? (2) Aの箱には何本の当たりくじが入っているでしょう? |
解答例1(ミミズクはくず耳さん、あんみつさん、あまれっとさん、ゆんななこさん、高橋道広さん、ヒッピーさん、バーニィさん、Figoさん、他)
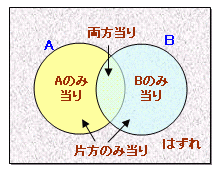
箱Aの当たりくじをa本、箱Bの当たりくじをb本とし、当たる確率をベン図で考えます。
両方当たる確率=a/30×b/30=1/10
よって、a×b=90 ・・・(1)Aのみ当たる確率=a/30×(1-b/30)、
Bのみ当たる確率=(1-a/30)×b/30、
よって、片方のみ当たる確率
=a/30×(1-b/30)+(1-a/30)×b/30
=a/30+b/30−a/30×b/30×2=17/30
従って、
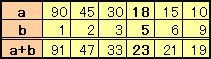
a+b=17+1/10×2×30=23 ・・・(2)90を素因数分解すると、
90=1×90、 2×45、 3×30、 5×18、 6×15、 9×10
となります。
この中で足して23になるのは5×18のみ。
題意より、a>bだからa=18、b=5。
答:(1)23本 (2)18本
以上
解答例2(takuさん、N.Nishiさん、中川幸一さん、名倉っちさん、tekiさん、M.Hossieさん、DrKさん、みーちゃんぶちゅさん、Parpunteさん、有無相生さん、巷の夢さん、銀次さん、うっしーさん、大岡敏幸さん、 他)
解答例1の(1)、(2)より、2次方程式の根と係数の関係を用いると、
a、bは、x2-23x+90=0の2根となります。よって、x=(23±√(232-4×90))/2=(23±13))/2=18、5
題意より、a>bだからa=18、b=5。
解答例3(Taroさん、名倉っちさん、ちば けいすけさん、他)
解答例1同様ベン図から、
少なくともどちらかが当たる確率
=片方のみ当たる確率+両方当たる確率
=17/30+1/10
=20/30よって、どちらもはずれる確率
=(1-a/30)×(1-b/30)=1-20/30=1/3
従って、
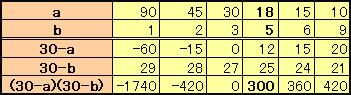
(30-a)×(30-b)=1/3×30×30=900 ・・・(3)
積が90となる整数a、b(a>b)の組み合わせで、(3)を満たすものは、
a=18、b=5のみである。