第279問の解答
問題 [整数の性質]
|
一の位の数が7の整数Aがあります。 この整数Aの一の位の数(7)を先頭に移動してできる数は、もとの整数Aの5倍であるそうです。 このとき、もとの整数Aとして考えられる数のうち、最も小さい数を求めなさい。 |
解答例1
(CRYING
DOLPHINさん、むらかみさん、ちーくんさん、ドッペンさん、あまれっとさん、角田(^^)v鉄也さん、Taroさん、まおさん、ちば
けいすけさん、ハラギャーテイさん、有無相生さん、航介さん、みーちゃんぶちゅさん、N.Nishiさん、ruruさん、大岡敏幸さん、他)
題意より、
○○○○○7×5=7○○○○○、または
7○○○○○÷5=○○○○○7
となります。
(掛け算で考える)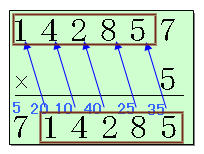 |
(割り算で考える)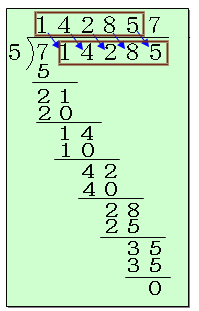 |
(掛け算で考える)
- ・十の位:
一の位の7に5を掛けて、7×5=35、
よって十の位は5となり、3が繰り上がります。
- ・百の位:
十の位の5に5を掛けて、5×5=25、
よって5に繰り上がりの3を加えて百の位は8、
2が繰り上がります。
- ・千の位:
百の位の8に5を掛けて、8×5=40、
よって0に繰り上がりの2を加えて千の位は2、
4が繰り上がります。
- ・万の位:
千の位の2に5を掛けて、2×5=10、
よって0に繰り上がりの4を加えて万の位は4、
1が繰り上がります。
- ・十万の位:
万の位の4に5を掛けて、4×5=20、
よって0に繰り上がりの1を加えて十万の位は1、
2が繰り上がります。・最後: 十万の位の1に5を掛けて、1×5=5、
よって5に繰り上がりの2を加えて7となるので、
求める整数Aは142857と分かります。
(割り算で考える)
- ・先頭の位:
7を5で割った商の1が先頭の位、
残余は7−5=2と1より21。
- ・2番目の位:
21を5で割った商の4が2番目の位、
残余は21−20=1と4より14。- ・3番目の位:
14を5で割った商の2が3番目の位、
残余は14−10=4と2より42。- ・4番目の位:
42を5で割った商の8が4番目の位、
残余は42−40=2と8より28。- ・5番目の位:
28を5で割った商の5が5番目の位、
残余は28−25=3と5より35。- ・6番目の位:
35を5で割ると商が7で、ちょうど割り切れるので、
求める整数Aは142857と分かります。答:142857
以上
解答例2
(ヒデー王子さん、トトロ@Nさん、きょえぴさん、中村明海さん、BossFさん、長野美光さん、永井
暁さん、
他)
整数Aの7以外の部分をPとし、その桁数をnとすると、
A=P×10+7
A×5=7×10n+P
と表すことができます。よって、
(P×10+7)×5=7×10n+P
P×49+7×5=7×10n
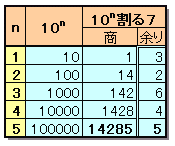
P×7+5=10n ・・・ (1)従って、10nは7で割った余りが5となります。
よって、n=5、P=14285、
従って、A=P×10+7=142857。
(別解)
(1)より、
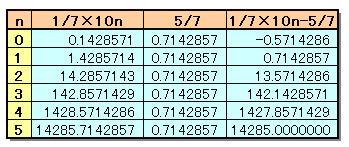
P=10n×1/7-5/7 ・・・ (2)ところが、
1/7=0.142857142857・・・
5/7=0.714285714285・・・
といずれも6桁の数字による循環数となります。1/7を10倍ずつするごとに1桁ずれていきます。このとき、(2)より、小数部が5/7と等しくなる必要があります。
5桁だけ、ずらしたとき、
1/7×105=14285.714285・・・
となるので、
P=1/7×105−5/7=14285。
従って、A=P×10+7=142857。