第280問の解答
問題 [平面図形]
|
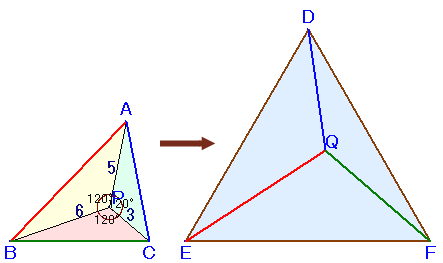
上の左図のような△ABCがあります。 いま、△ABCの内部に点Pをとったところ、AP=5cm、BP=6cm、CP=3cmとなり、 ∠APB=∠BPC=∠CPA=120度となりました。 また、右図のような正三角形DEFを作ります。 この正三角形DEFは、その内部に点Qをとると、DQ=AC、EQ=AB、QF=BCとなります。 では、正三角形DEFの面積は、△ABCの何倍でしょうか。 |
解答例1(トトロ@Nさん、 他)
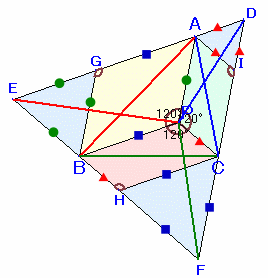
△ABQ、△QBC、△AQCをそれぞれ△ABCの外側に点対称となるようにおいたものを、△AGB、△BHC、△ACIとします。
すると、四角形AGBQ、四角形QBHC、四角形AQCIは平行四辺形になります。
また、AG、BH、CIを延長して交わった点をD、E、Fとします。
∠AGB=∠AQB=120度より、∠BGE=60度。
∠GBQ=∠GBA+∠ABQ=∠BAQ+∠ABQ=60度。
同様に、∠QBH=60度。
従って、∠GBE=60度。
以上より、△GEBは正三角形となります。同様に、△CHF、△DAIも正三角形となります。
従って、△DEFが求める正三角形となり、
△DEF=△ABC×2+△GEB+△CHF+△DAI△DEFの一辺は3+5+6=14cmなので、
△DEF/△ABC
=142/{(142-32-52-62)/2}
=196/63
=28/9
となります。答:28/9倍
以上
解答例2
(KINさん、うっしーさん、CRYING DOLPHINさん、ヒデー王子さん、きょえぴさん、ちば けいすけさん、高橋道広さん、有無相生さん、N.Nishi
さん、あやのりんさん、あまれっとさん、他
多数)
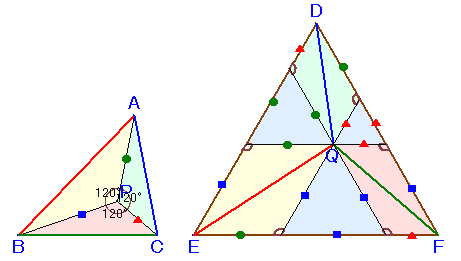
上図のように考えると、解答例1と同様に、
△DEF/△ABC
=142/{(142-32-52-62)/2}
=196/63
=28/9
となります。
解答例3 (AЯCさん、他)
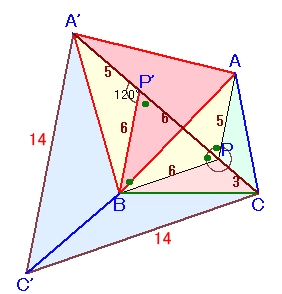
点Bを中心に△ABPを反時計回りに60度回転したものを△A'B'Pとします。
すると、△AA'Bと△PP'Bは正三角形となります。
また、
∠A'P'B+∠PP'B=120+60=180度、
∠P'PB+∠BPC=60+120=180度より、
A'、P'、P、Cは一直線上に並びます。
A'C=AP'+P'P+PC=AP+BP+CP=5+6+3=14cm。点A'を中心に△AA'Cを時計回りに60度回転したものを△BAC'とします。
すると、△C'A'Cが求める正三角形DEFとなることが分かります。1辺が1cmの正三角形の面積を1とおくと、
∠ABP=∠BPC=∠APC=120度より、
△ABP=5×6=30、△PBC=6×3=18、△APC=3×5=15。従って、
△DEF/△ABC
=14×14/(30+18+15)
=28/9
となります。