第２８１問の解答

---

問題　［平面図形］

左図のようなＡＢ＝ＣＤ＝５cmの平行四辺形ＡＢＣＤがあります。 いま、辺ＡＤの中点Ｍと頂点Ｃを結び、線分MC上の点Ｐと頂点Ａを結びました。すると、ＡＰ＝ＡＢ（＝５cm）、ＭＰ＝２cm、ＰＣ＝４cmとなりました。 このとき、平行四辺形ＡＢＣＤの面積を求めて下さい。

---

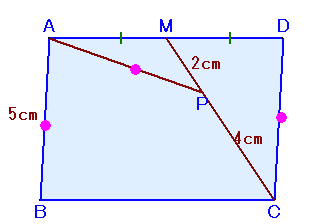解答例１(Taroさん、ヒデー王子さん、CRYING DOLPHINさん、名倉っちさん、永井暁さん、きょえぴさん、高橋道広さん、あやのりんさん、あまれっとさん、Parpunteさん、萬田銀次郎さん、他多数)

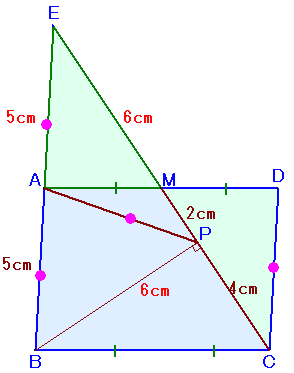
△CDMを１８０度回転し、辺DMをAMにくっつけたものを△ECMとします。

∠EAM＋∠MAB＝∠CDM＋∠MAB＝１８０度、
∠EMA＋∠AMC＝∠CDM＋∠AMC＝１８０度、
より、三点E、A、BおよびE、M、Cは一直線上に並びます。

△EBPにおいて、EA＝AB＝AP＝５ｃｍより、∠APBは直角になります。
（∠EPA＋∠APB＝（∠PAB＋∠EAP）×1/2＝９０度）

EB＝EA＋AB＝CD＋AB＝５＋５＝１０ｃｍ、
EP＝EM＋MP＝CM＋MP＝６＋２＝８ｃｍ。
従って、△EBPは辺の長さが３：４：５の直角三角形と相似。
よって、BP＝６ｃｍとなります。

よって、
　平行四辺形ABCDの面積
＝△EBC
＝1/2×EC×BP
＝1/2×１２×６
＝３６ｃｍ²
となります。

なお、直線BA、CMの交点をEとする方法でも、△EAM≡△CDMより上記同様に求まります。
　

答：３６cm²

以上

---

解答例２　(トトロ＠Ｎさん、takuさん、ふじさきたつみさん、ばつ丸さん、 他)

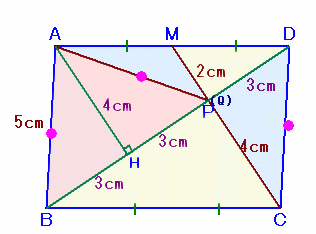
対角線ＢＤと辺ＭＣの交点をＱとします。

△ＱＢＣと△ＱＤＭは相似で比はＢＣ：ＤＭ＝２：１。
従って、ＣＱ：ＱＭ＝２：１。
よって、ＣＱ＝４ｃｍ、ＱＭ＝２ｃｍとなり、ＱとＰは一致します。
また、ＢＰ：ＰＤ＝２：１。

△ＡＢＰはＡＢ＝ＡＰ＝５ｃｍの二等辺三角形より、
点ＡからＢＰにおろした垂線の足をＨとすると、ＢＨ＝ＨＰ。
よって、ＢＨ＝ＨＰ＝ＰＤとなります。

ＤＭ：ＭＡ＝ＤＰ：ＰＨより、△ＤＭＰと△ＤＡＨは相似、
よって、ＡＨ＝ＭＰ×２＝２×２＝４ｃｍ。
従って、△ＡＢＨ、△ＡＰＨは辺の長さが３：４：５の直角三角形。

よって、ＢＤ＝ＢＨ＋ＨＰ＋ＰＤ＝３×３＝９ｃｍ。
　平行四辺形ＡＢＣＤの面積
＝△ＡＢＤ×２
＝1/2×ＢＤ×ＡＨ×２
＝1/2×９×４×２
＝３６ｃｍ²
となります。

---

解答例３　(sugitakukunさん、中川幸一さん、アークさん、他)

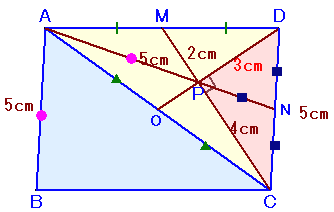
ＡＰの延長線とＣＤの交点をＮ、およびＤＰの延長線とＡＣの交点をＯとします。

ＡＭ＝ＭＤ、ＣＰ：ＰＭ＝４：２＝２：１より点Ｐは△ＡＣＤの重心となります。
よって、ＤＮ＝ＮＣ＝２．５ｃｍ、ＰＮ＝ＡＰ×1/2＝２．５ｃｍ。
従って、∠ＤＰＣ＝９０度となります。

よって、△ＤＰＣは辺の長さが３：４：５の直角三角形となり、
辺ＤＰ＝３ｃｍとなります。

従って、△ＭＣＤ＝1/2×ＭＣ×ＤＰ＝1/2×６×３＝９ｃｍ²。

　平行四辺形ＡＢＣＤ
＝△ＡＣＤ×２
＝△ＭＣＤ×４
＝３６ｃｍ²。

---

解答例４　(有無相生さん、他)

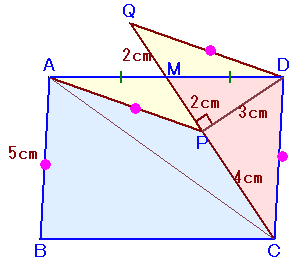
点Ｄを通り辺ＰＡと平行に引いた直線と辺ＣＭの延長線を点Ｑとします。

ＱＤとＡＰが平行でＡＭ＝ＭＤより△ＱＭＤ≡△ＰＭＡ。
よって、ＱＭ＝ＰＭ＝２ｃｍとなります。

すると、△ＤＱＣはＤＱ＝ＤＣ＝５ｃｍの二等辺三角形で、
しかも、ＱＰ＝ＰＣ＝４ｃｍより、点Ｐは辺ＱＣの中点、
よって、ＤＰ⊥ＱＣとなります。

従って、△ＤＰＣは辺の長さが３：４：５の直角三角形となり、
辺ＤＰ＝３ｃｍと分かります。

以下、解答例３と同じ。

---