第２８３問の解答

---

問題　［整数の性質］

１０００以上２０００以下の整数の中から、２個の連続した整数の組を選びます。 その２個の整数の和（足し算）を計算するとき、どのケタでも繰りあがりが起こらない組は何通り選ぶことができるでしょうか。

---

解答例１(Taroさん、ミミズクはくず耳さん、sodoさん、ちーくんさん、小杉原啓さん、noetherさん、辻。さん、まおさん、倉澤将司さん、名倉っちさん、うっしーさん、トトロ＠Ｎさん、老人拳！さん、永井暁さん、takuさん、まちゅだちんやさん、角田(＾＾)v鉄也さん、モルモット増殖中さん、きょえぴさん、アークさん、M.Hossieさん、あまれっとさん、有無相生さん、 他多数)

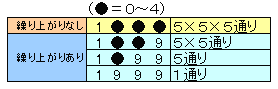
１位の数を考えると、
　・繰り上がりなしのとき：0+1=1、1+2=3、2+3=5、3+4=7、4+5=9　・・・　５通り
　・繰り上がりありのとき：9+0=9　　　　　 　　　　　　　　　　　　　　・・・　１通り
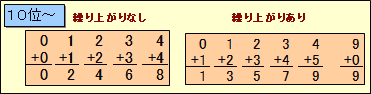
が考えられます。

１０位より上の数では、
　・１位の数で繰り上がりのないとき：
　　0+0=0、1+1=2、2+2=4、3+3=6、4+4=8　・・・　５通り
　・１位の数で繰り上がりがあるとき：
　　0+1=0、1+2=3、2+3=5、3+4=7、4+5=9　・・・　５通り および　9+0=9の１通り

従って、上表のように分類すると、求める組み合わせの数は
　５×５×５＋５×５＋５＋１＝１５６通り
となります。

　

答：１５６通り

以上

---

解答例２(DrKさん、 他)

先頭の１以外の桁数がnのとき、組み合わせの数をF(n)として漸化式で考えます。

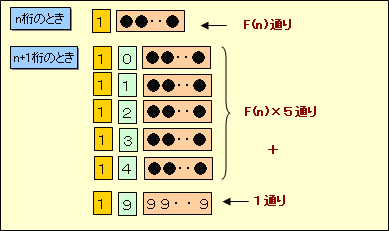
・n=0のとき、１+2=3の１通り。よって、F(1)=1。

・F(n)まで求まるとき、F(n+1)は、
　２桁目が０〜４のとき、それぞれF(n)通り
　２桁目が９のときで残りの桁も全て９の１通り　
したがって、　F(n+1)＝F(n)×５＋１　・・・　（１）　となります。

（１）より、順次求めていくとF(3)=156通りとなります。

なお、一般式は次のようにして求まります。
（１）より、
　F(n)＋1/4＝(F(n-1)+1/4）×５＝・・・＝(F(0)+1/4)×５ⁿ＝1/4×５ⁿ⁺¹
よって、
　F(n)＝1/4×（５ⁿ⁺¹−1）

---