第２８４問の解答

問題　［平面図形］

問題図

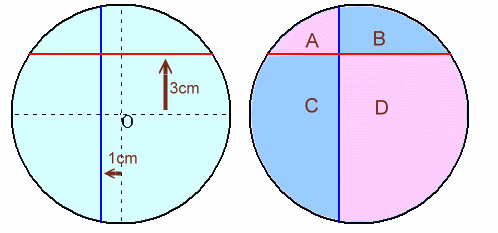
上図のような円があります。

いま、この円を左の図のような２本の直線で４つの部分Ａ〜Ｄに分けます。
赤い直線は、水平方向にひいた直径を上のほうに３cmだけ平行移動したもの、
青い直線は、垂直方向に引いた直径を左のほうに１cmだけ平行移動させたものです。

このとき、右の図のＡの部分とＤの部分の面積の和（桃色の部分）は、Ｂの部分とＣの部分の面積の和（水色の部分）と比べて、何cm2だけ大きいでしょうか。

解答例１(takuさん、C-Dさん、トトロ＠Ｎさん、モルモット大臣さん、角田(＾＾)v鉄也さん、さとけんさん、BossFさん、ふじさきたつみさん、tapuさん、あまれっとさん、有無相生さん、M.Hossieさん、大岡敏幸さん、DrKさん、長野美光さん、ss7さん、なみどんさん、あやのりんさん、 他多数)

参考図１

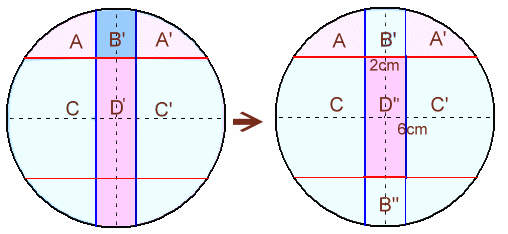
まず、縦の中心線を軸にして、右側の部分から左側の部分を差し引きます。
　B'＝B−A
　D'＝D−C

今度は、横の中心線を軸にして、下側の部分から上側の部分を差し引きます。
残った２cm×６cmの長方形D''の面積が求める面積に等しくなります。
　D''＝D'−B'
　　＝（D-C）−（B-A）
　　＝（A＋D）−（B＋C）
　　＝２×６
　　＝１２cm2

答：１２cm2

以上

（その他の解法）

・三角関数を使って解く　・・・　中川　幸一さん他