第２８５問の解答

---

問題　［平面図形］

次の条件を満たす２ケタ以上の整数はいくつあるでしょうか。 ［条件］どの位の数字をとっても、その右側にあるどの数よりも大きい。

---

解答例・・・今回は、解説風にしてみました。

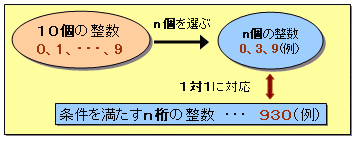
条件を満たすｎ桁の整数(2≦n≦10)は、１０個の整数０、１、・・・、９からｎ個選んで数字の大きい順に並べたものと１対１に対応します。

従って、１０個のものからｎ個選ぶのは、₁₀C_n＝10!/(10-n)!n!と表されるので、求める個数は、
₁₀C₂＋₁₀C₃＋・・・＋₁₀C₁₀・・・　（１）
＝４５＋１２０＋・・・＋１
＝１０１３個
となります。

直接（１）式を計算した方（手計算またはＥＸＣＥＬなど）　・・・

　長野美光さん、トトロ＠Ｎさん、Miki Sugimotoさん、ＡЯＣさん、ミミズクはくず耳さん、辻。さん、プラスアルファさん、あまれっとさん、他

　

（１）式を２項定理を利用して計算した方　・・・

　Taroさん、noetherさん、Miki Sugimotoさん、中川幸一さん、きょえぴさん、N.Nishiさん、QPerさん、Parpunteさん、takuさん、萬田銀次郎さん、いごまるさん、他

　　₁₀Ｃ₂＋₁₀Ｃ₃＋・・・＋₁₀Ｃ₁₀
＝（₁₀Ｃ₀＋₁₀Ｃ₁＋₁₀Ｃ₂＋₁₀Ｃ₃＋・・・＋₁₀Ｃ₁₀） −（₁₀Ｃ₀＋₁₀Ｃ₁）
＝２¹⁰-(10+1)
＝1024-11
＝1013　個

　

（参考）２項定理
　（x＋y）ⁿ＝_nＣ_nxⁿ＋_nＣ_n-1x^n-1y＋_nＣ_n-2x^n-2y²＋・・・＋_nＣ₁xy^n-1＋_nＣ₀yⁿ

２項定理は、x^n-ky^kの係数は、n個のxからk個選び、残り(n-k)個のyと掛け合わすことと考えることで導くことができます。

とくに、x＝y＝1、n＝10のとき、
　２¹⁰＝₁₀Ｃ₁₀＋₁₀Ｃ₉＋₁₀Ｃ₈＋・・・＋₁₀Ｃ₁＋₁₀Ｃ₀
となります。

　

算数で考えた方　・・・

　高橋道広さん、ふじさきたつみさん、他

ｎ桁の整数(0≦n≦10)は、１０個の整数０、１、・・・、９からｎ個選ぶのは、
　０を選ぶか選ばないの２通り×・・×９を選ぶか選ばないの２通り
＝２¹⁰＝１０２４通りと求まります。

これから、n=0の１通り、n=1の１０通りを除くと1024-11=1013個と計算できます。

答：１０１３個

以上

---

（その他の解法）

・０が入るか否かで場合分け　・・・　C-Dさん他

（２^9−１０）×２＋９＝１０１３

　

・樹形図を描いて規則性を見出す　・・・　M.Hossieさん他

１の桁に８をおくと、９８の１通り。
１の桁に７をおくと、９８７，８７，９７の３通り。
こんな感じで書いていくと、規則性が分かってきて、2^k -1 通り。

１の桁は８から０までの９通りあり、kは1〜9までだから、その合計を計算して、Σ_[k=1,9] (2^k - 1) = 1013 通り

---