第２８８問の解答

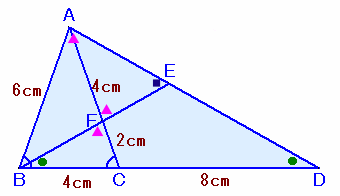
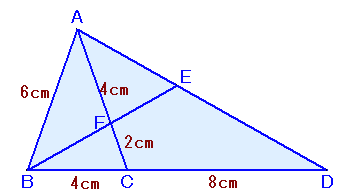
問題　［平面図形］

左図のようなＡＢ＝ＡＣ＝６cm、ＢＣ＝４cmの二等辺三角形ＡＢＣがあります。

いま、この二等辺三角形の辺ＡＣ上に、ＡＦ＝４cmとなる点Ｆを、辺ＢＣの延長上に、ＣＤ＝８cmとなる点Ｄをとります。ＢとＦを結んだ直線がＡとＤを結んだ直線と交わる点をＥとします。

このとき、ＡＥの長さはＦＥの長さの何倍でしょうか。

解答例１（CRYING DOLPHINさん、他）

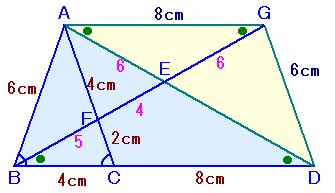
Ａを通りＢＤと平行な線と、ＢＥの延長線との交点をＧとします。

参考図１

まず、△ABCはAB＝AC＝６ｃｍより二等辺三角形、
よって、∠ABC＝∠ACB。　・・・　（１）

△BCFと△DBAについて、
　∠BCF＝∠DBA（（１）より）、BC：CF＝DB：BA＝２：１
より、△BCF∽△DBA、従って、∠CBF＝∠BDA。

よって、△EBDはEB＝EDの二等辺三角形。　・・・　（２）

AGとBDは平行だから、△FBC∽△FGA、
よって、
　AG＝BC×FA/FC＝４×４/２＝８ｃｍ、
　BF：FG＝FC：FA＝１：２。　・・・（３）

同様に、AGとBDは平行だから、△EAG∽△EBD。
よって、BE：EG＝BD：AG＝１２：８＝３：２。

従って、BE＝９とおくとEG＝AE＝６。　・・・（４）

（３）より、BF＝BG×１/３＝５、
　FE＝BE−BF＝４。　・・・（５）

よって、（４）、（５）より、
　AE/FE＝６/４＝３/２。

答：３/２

以上

解答例２（高田修成さん、前田先生＠P進学院さん、 他）

参考図２

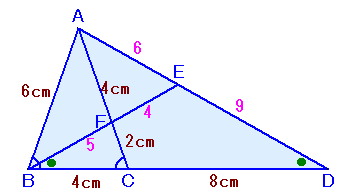
△ＡＢＤと△ＦＣＢが相似で、△ＥＢＤが二等辺三角形
までは、解答例１と同じ。

△ACDと直線BEについて、メネラウスの定理より、
　AF/FC×CB/BD×DE/AE＝１、
　４/２×４/１２×DE/AE＝１、
よって、DE：AE＝３：２。

従って、ED＝EB＝９とおくと、AE＝９×２/３＝６。　・・・（１）

また、 △EBDと直線ACについて、メネラウスの定理より、
　EF/FB×BC/CD×DA/AE＝１、
　EF/FB×４/８×１５/６＝１、
よって、EF：FB＝５：４、
従って、FE＝EB×４/９＝４。　・・・（２）

（１）、（２）より、
　AE/FE＝６/４＝３/２。

解答例３（角田(＾＾)v鉄也さん、他）

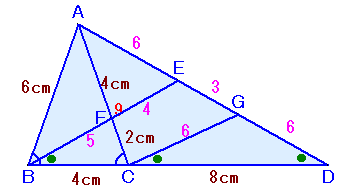
Cを通ってBEと平行な直線とADの交点をGとします。

参考図３


△ＡＢＤと△ＦＣＢが相似で、△ＥＢＤが二等辺三角形
までは、解答例１と同じ。

EBとGCは平行だから、△GCDは△EBDと相似な二等辺三角形。
そこで、EB＝ED＝９とおくと、
　GD＝ED×CD/BD＝９×２/３＝６、
　EG＝ED−GD＝９−６＝３。

FEとCGは平行だから、△AFEと△ACGは相似、
よって、AE：EG＝AF：FC＝２：１、　AE＝EG×２＝６。　・・・（１）
また、FE：CG＝AF：AC＝２：３、　FE＝CG×２/３＝４。・・・（２）

（１）、（２）より、　AE/FE＝６/４＝３/２。

解答例４（シイサンさん、他）

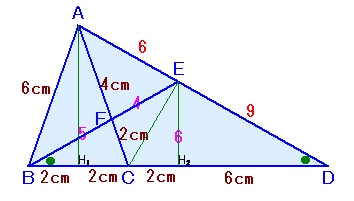
AおよびEからBDにおろした垂線の足をH1、H2とします。

参考図４

△ＡＢＤと△ＦＣＢが相似で、△ＥＢＤが二等辺三角形
までは、解答例１と同じ。

△ABCの面積を５とおくと、
△ACD：△ABC＝CD：BC＝８：４＝２：１、
よって、△ACD＝△ABC×２＝１０。

△ABCおよび△EBDは、ともに二等辺三角形より、
　H1およびH2は、それぞれBCおよびBDの中点、
よって、BH1＝H1C＝２ｃｍ、BH2＝H2D＝６ｃｍ。

△AH1Dと△EH2Dは相似より、
　AE：ED＝H1H2：H2D＝４：６＝２：３。

よって、ED＝９とおくと、AE＝６。　・・・（１）

従って、△CAE：△CDE＝AE：ED＝２：３、
よって、△CAE＝４。

さて、BF：FE＝△ABC：△ACE＝５：４。
EB＝ED＝９より、FE＝EB×４/９＝４。　・・・（２）

（１）、（２）より、　AE/FE＝６/４＝３/２。

解答例５
（まるケンさん、M.Hossieさん、ちば けいすけさん、岩間美顕さん、永井暁さん、ななしひめさん、算数野郎小６さん、 他）

参考図５

△ＡＢＤと△ＦＣＢが相似で、△ＥＢＤが二等辺三角形
までは、解答例１と同じ。

従って、∠ＢＡＤ＝∠ＣＦＢ。 　・・・（１）

△ＢＡＥと△ＡＦＥについて、
　∠BAE＝∠CFB＝∠AFE、∠AEBは共通、
より相似。

従って、AE：FE＝BA：ＡＦ＝６：４＝３：２。

解答例６（ふじさきたつみさん、他）

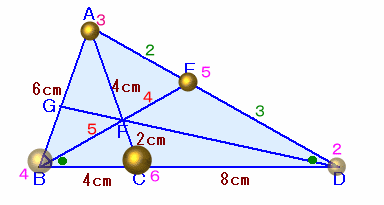
天秤法（チェバの定理の応用）で考えます。

参考図６

△ＡＢＤと△ＦＣＢが相似(相似比は、３：１)で、△ＥＢＤが二等辺三角形
までは、解答例１と同じ。

AF：FE＝２：１なので、Fで釣り合うようにAとCにおもりを置くと、
おもりの比は１：２。
そこで、Aに置くおもりを３、Cに置くおもりを６とします。

次に、Cのおもり６をBとDに分けてCで釣り合わせるためには、
　BC：CD＝１：２なので、おもりの比は２：１、
従って、Bのおもり４、Dのおもり２となります。

よって、FでAとDのおもりが釣り合うことから、
　AF：FD＝３：２。

今度はAとDのおもりを合わせてEにおくと重さは３＋２＝５。
これとBのおもりがFで釣り合うことから、
　BF：FE＝５：４。

そこで、EB＝ED＝９とおくと、
　AF＝ED×２/３＝９×２/３＝６、
　FE＝EB×４/９＝９×４/９＝４。

よって、AF/FE＝６/４＝３/２。

（その他の解法）

・ベクトルを用いる　・・・　ＡЯＣさん、QPerさん 、有無相生さん、他

・メネラウスの定理、余弦定理などを用いる　・・・　うっしーさん 、ハラギャーテイさん、他

・座標を用いる　・・・　モルモット大臣さん、Parpunteさん、他