第２８９問の解答

問題　［整数の性質］

次のような形の循環小数を考えます。

　０．■▲■▲■▲■▲■▲・・・・（ただし、■と▲は異なる１ケタの整数）

このような循環小数のうち、分数に直して出来る限り約分したときにできる分子の数字は、
全部で何通りあるでしょうか。

解答例１（小杉原啓さん、トトロ＠Ｎさん、ちーくんさん、まるケンさん、あんみつさん、高橋道広さん、FALCONさん、他 多数）

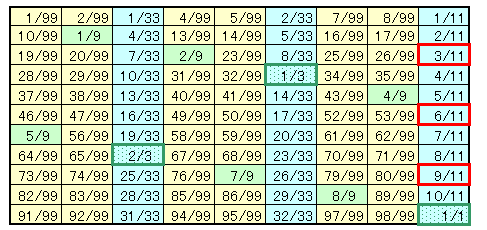
このような循環小数は、N=ｎ/９９（1≦n≦98）の形をしています。
なぜなら、
　　　　N=　　０．■▲■▲■▲■▲・・・　　（１）
１００×N=■▲．■▲■▲■▲■▲・・・　　（２）
よって、（２）−（１）より、
　　９９×N＝■▲
　　N=■▲/９９

まず、■と▲は異なるので、ｎは１１の倍数ではありません。

また、ｎが３の倍数のとき、ｎ＝３×ｐとすると、（ｐは１１の倍数でない）
　ｎ/９９＝３×ｐ/９９＝ｐ/３３
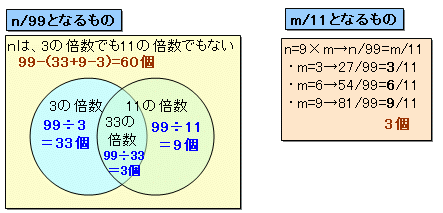
となり、ｎが分子の数字にはなり得ませんので除く必要があります。　・・・　（３）

従って、ｎ/９９の形をしたものは、３の倍数でも１１の倍数でもない整数で、
　３の倍数＝９９÷３＝３３個
１１の倍数＝９９÷１１＝９個
３３の倍数＝９９÷３３＝３個
より、９９−（３３＋９−３）＝６０個あります。

参考図１

（３）で、もしｐが３の倍数（ｎは９の倍数＝９×ｍ）とすると、
　Ｎ＝９×ｍ／９９＝ｍ／１１
の形になります。
このとき、１≦ｍ≦８で、ｍが３の倍数のとき（ｍ＝３、６、９）には、（３）で除いた分子の数字を実現することになるので、この３個を加える必要があります。

参考図２


従って、合計６０＋３＝６３通りあることになります。

答：６３通り

以上