第２９０問の解答

問題　［ 空間図形］

問題図

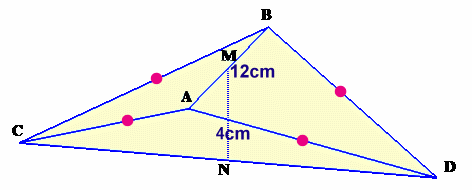
四面体ＡＢＣＤのＡＢの中点をＭ、ＣＤの中点 をＮとするとき、ＡＢ＝１２cm、ＭＮ＝４cm、ＡＣ＝ＢＣ＝ＡＤ＝ＢＤとなっています。

この四面体を直線ＭＮを軸に９０度回転して、元の四面体と重なる部分の体積が１０８cm3であったそうです。

では、四面体ＡＢＣＤの体積は何cm3でしょうか。

解答例１（ヒデー王子さん、C-Dさん、あんみつさん、ｍａｓａｓｈｉさん、ちーくんさん、sodoさん、角田(＾＾)v鉄也さん、まおさん、ミミズクはくず耳さん、ふじさきたつみさん、小西孝一さん、長野美光さん、ちば けいすけさん、他 多数）

参考図１

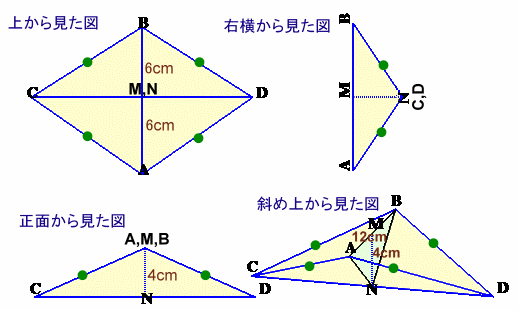
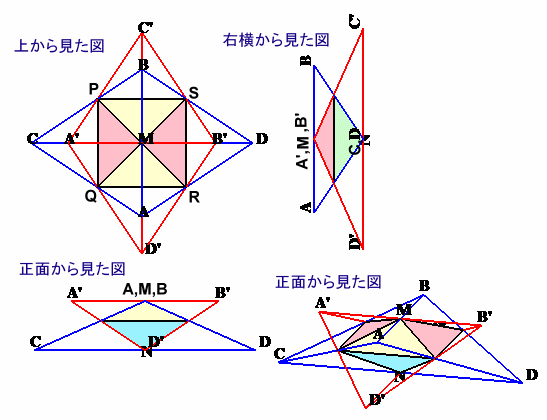
対象性より、上から見るとＢＣＡＤは菱形になり、△ＡＢＮ（二等辺三角形）と辺ＣＤは直交していることが分かります。

従って、これを９０度回転して重ねた立体は、上から見ると正方形（ＰＱＲＳとします）を底辺とする２つの四角錐Ｍ−ＰＱＲＳ、Ｎ−ＰＱＲＳを合わせたものになります。

参考図２

この立体の体積は、1/3×正方形ＰＱＲＳの面積×ＭＮ＝１０８ｃｍ3となることから、
正方形ＰＱＲＳの面積＝１０８×３／４＝８１ｃｍ2。

従って、正方形ＰＱＲＳの１辺の長さは、９ｃｍと分かります。

参考図３ 参考図４

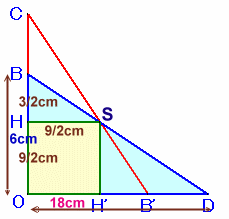
平面ＰＱＲＳで切断したものの1/4をみると、
ＢＯ＝ＡＢ×1/2＝６ｃｍ、ＨＯ＝ＨＯ'＝ＰＳ×1/2＝9/2ｃｍ、
よって、ＢＨ＝ＢＯ−ＨＯ＝3/2ｃｍ。

△ＢＨＳと△ＢＯＤは相似だから、ＢＯ：ＯＤ＝ＢＨ：ＨＳ＝１：３、
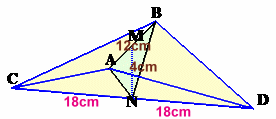
よって、ＯＤ＝ＢＯ×３＝１８ｃｍ。

元の四角形ＡＢＣＤは、２つの合同な三角錐Ｃ−ＡＢＮ、Ｄ−ＡＢＮを合わせたものだから、体積＝1/3×△ＡＢＮ×ＮＤ×２＝1/3×２４ｃｍ2×１８ｃｍ×２＝２８８ｃｍ3となります。

答：２８８cm3

以上

（参考）動く３Ｄ図

（その他の解法）

・四角錐台（上面の正方形の対角線が１２cm、下面の対角線が３６cm、高さが４cm）からの切断で考える
　・・・　トトロ＠Ｎさん