第２９１問の解答

---

問題　［ 空間図形］

球を１０個の平面で切断したとき、表面は最大何個の破片に分かれるでしょうか。

---

解答例１（ミミズクはくず耳さん、takuさん、CRYING DOLPHINさん、角田(＾＾)v鉄也さん、中学への算数さん、高橋道広さん、ちば けいすけさん、トトロ＠Ｎさん、中村明海さん、Parpunteさん、 他 多数）

n個の平面で切断したときの破片数をF_nとし、nに関する漸化式で考えます。

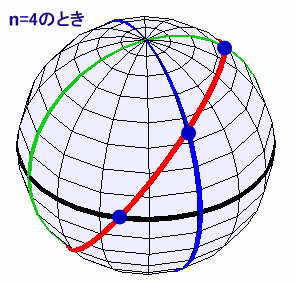
n=１のとき、F₁＝２。　・・・　（１）

n≧2のとき、n個めの平面で切断すると、それまでの（n-1）個の平面と２回ずつ交わるので、（n-1）×２個の破片が増える。

従って、F_n＝F_n-1＋２（n-1）　・・・　（２）

（１）、（２）より、順次計算して求めると、F₁₀＝９２となります。

　

なお、一般式は、
　F_n＝F₁＋Σ_k=2..n（F_k−F_k-1）
＝２＋２Σ_k=2..n（k-1）
＝（n-1）n＋２
となります。本問の場合、F₁₀＝９×１０＋２＝９２。
　

答：９２個

以上

---

解答例２（あんみつさん、ＡЯＯＴさん、前田先生＠P進学院さん、まおさん、岩間美顕さん、小西孝一さん、ふじさきたつみさん、 他 多数）

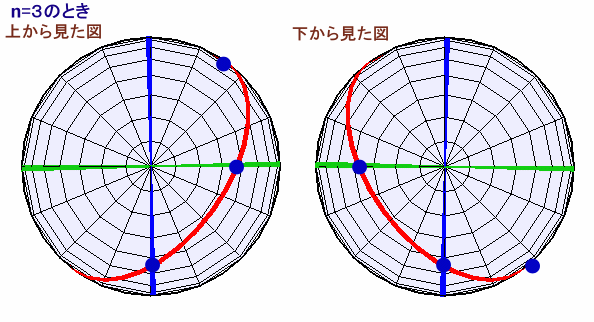
最初に水平な面（黒色）で切断した２つの面で考えます。

これ以降、平面で切断したときの破片数（G_nとします）は等しいので、
　F_n＝G_n-1×２
となります。

G₁＝２、G_n＝G_n-1＋nより、G₉＝４６、
よって、F₁₀＝G₉×２＝９２個となります。

なお、一般式は、
　G_n＝G₁＋Σ_k=2..n（G_k−G_k-1）
＝２＋Σ_k=2..nk
＝１＋Σ_k=1..nk
＝n（n＋1）×1/2＋１
となります。

これより、
　F_n＝G_n-1×２＝（n−１）ｎ＋２
を得ます。

---