第２９３問の解答

問題　［ 場合の数］

上の図のように、正方形のマス目が横に８つ並べられています。

  • まず、この８つのマス目のどれかに数字の１を記入します。

  • 次に、数字の２を、１が記入されたマス目の隣（左右どちらか）に記入します。

  • 次に、数字の３を、１または２のどちらかの隣に記入します。

  • ４〜８の数字も順に同様に、数字がかかれたマス目の隣に記入するようにします。

　このようにしたときできる数字の並び方は何通り考えられますか。

　

解答例１（ミミズクはくず耳さん、長野美光さん、真島嘉弘TZさん、トトロ＠Ｎさん、中西りゅうさん、CRYING DOLPHINさん、QPerさん、角田(＾＾)v鉄也さん、高橋道広さん、H.Takaiさん、大岡敏幸さん、中村明海さん、YokoyaMacさん、他 多数）

参考図１

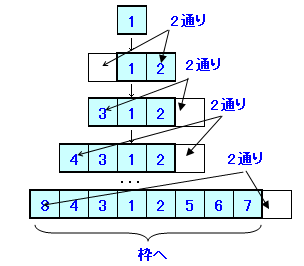
１を記入した後は、次の数字を記入する場所は左右２通りある。
従って、２から８の並べ方は２7＝１２８通り。

１から８まで記入した後で 横にずらして問題の８マスに入れればよい。
よって、求める場合の数も１２８通り。

答：１２８通り

以上

解答例２（Taroさん、sodoさん、モルモット大臣さん、前田先生＠Ｐ進学院さん、ねこやんさん、 他）

参考図２D

  • 1が一番左のとき　・・・　残りは全て決まるので、1通り

  • 1が左から2番目のとき　・・・　
    一番左にくる数を残りの７つの数字から１つ選ぶので、7C1＝7通り

  • 1が左から3番目のとき　・・・
    　1の左に残りの７つの数字から２つ選ぶので、7C２＝21通り

以後同様にして、求める場合の数は、
7C0+7C1+7C2+7C3+7C4+7C5+7C6+7C7＝２7＝１２８通り。

解答例３（ふじさきたつみさん、有無相生さん、あまれっとさん、 他）

漸化式で考えます。
マス目がn個のとき、場合の数をFnとします。

参考図３

nまでの数字をおくのは、

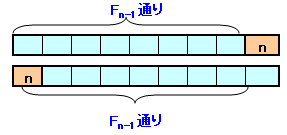
  • nが右端にくるとき　・・・　残りの（n-1）個のマス目には、Fn-1通り

  • nが左端にくるとき　・・・　残りの（n-1）個のマス目には、Fn-1通り

よって、Fn＝Fn-1×２。
従って、
　Fn＝（Fn/Fn-1）×（Fn-1/Fn-2）×・・・×（F2/F1）×F1
　　　＝２×２×・・・×２×１
　　　＝２7
　　　＝１２８通り。　

解答例４（ハラギャーテイさん、 他）

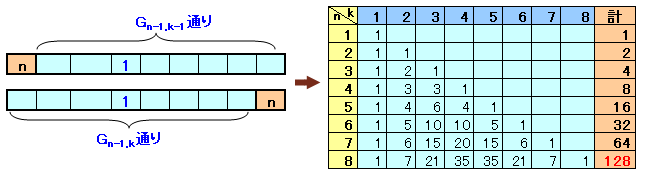
マス目がn個のとき、左からk番目のマス目に１をおくときの場合の数をGn,kとします。

参考図４

Gn,k＝Gn-1,k-1(nが左端のとき)＋Gn-1,k(nが右端のとき)
が成り立つので、順次計算していくと上表のようにして、
n=8のとき、合計１２８通りあることが分かります。

解答例５（Parpunteさん、 他）

下表のような経路図で考えます。

参考図５

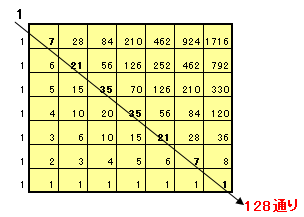
最初の１を置いたときを左下の交差点で表し、
次の数字を右に置く場合を右へ進む、左に置く場合を上に進むと表します。

すると、８個のマス目に数字をおくのは、左下から行程距離が７の交差点へ至る経路数となりますので、順次計算していくと、
１＋７＋２１＋３５＋３５＋２１＋７＋１＝１２８通りとなります。

（その他の解法）

・樹形図を用いて求める、場合分けして求める　・・・
　　M.Hossieさん 、ＮＡＴＵさん 、あんみつさん 、おかひで博士さん