第294問の解答
問題 [ 平面図形]
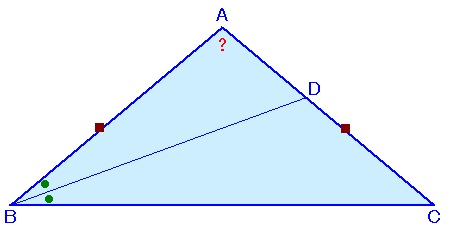
|
上の図は、AB=ACの二等辺三角形ABCを表しています。 |
解答例1(ふじさきたつみさん、モルモット大臣さん、他)
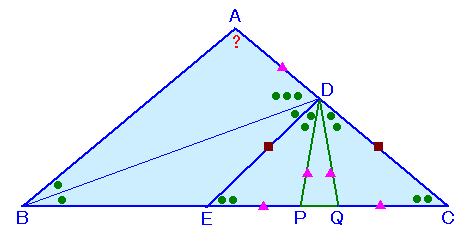
点DからBCに平行な線を引いてABとの交点をEとし、
BC上にCF=ADとなるFをとりDと結びます。また、∠DBC=θとおきます。
EDとBCは平行だから、△AEDは△ABCと相似な二等辺三角形。
よって、∠AED=∠ADE=∠ABC=∠ACB=2θ、
また、AE=AD、EB=DC。EDとBCは平行だから、∠EDB=∠DBF=∠EBD=θ、
よって、△EBDは二等辺三角形となり、EB=ED。また、△AEDと△FCDについて、
AE=AD=FC、ED=EB=CD、∠AED=∠FCD=2θ
と二辺挟角が等しいので合同。
従って、△FCDも二等辺三角形となり、
DF=FC、∠FDC=∠FCD=2θさて、題意よりBD+AD=BC=BF+FC、AD=FCだから、BD=BF。
よって、△BFDは二等辺三角形となり、∠BDF=∠BFD=∠FDC+∠FCD=4θ。従って、△BFDの内角の和=∠DBF+∠BDF+∠BFD=9θ=180度。
よって、θ=180度/9=20度。 ・・・ (1)∠BAC=180度−∠BAC−∠CAB=180度−4θ=100度。・・・ (2)
答:(1)20度 (2)100度
以上
解答例2(計算鑑定人さん、角田(^^)v鉄也さん、岩間美顕さん、数楽者さん、ねこやんさん、ぽんつくさん、他)
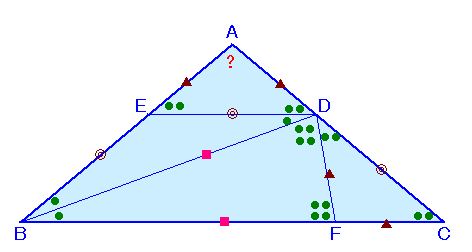
BC上にBP=ABとなる点P、CQ=ADとなる点Q、およびDE=DCとなる点Eをとります。 ∠DBE=∠ABD=θとします。
DE=DCより、△DECは二等辺三角形、
よって、∠DEC=∠DCE=2θ。∠BDE=∠DEC−∠DBE=2θ−θ=θ。
∠ADB=∠DBC+∠DCB=θ+2θ=3θ。△ABDと△PBDは合同より、AD=PD、∠ADB=∠PDB=3θ、
よって、∠EDP=∠PDB−BDE=3θ−θ=2θ。
従って、△PDEは、PE=PD=ADの二等辺三角形。
△DEPと△DCQについて、
DE=DC、EP=AD=CQ、∠DEP=∠DCQより、二辺挟角が等しいので合同。よって、△DCQもQD=QCの二等辺三角形。
従って、∠QDC=∠QCD=2θ。
よって、∠DQB=∠QDC+∠QCD=4θ。題意より、BD+AD=BQ+QC=BC、AD=QC、
よってBD=BQとなり、△BDQは、BD=BQの二等辺三角形。
従って、∠BDQ=∠BQD=4θ。∠ADB+∠BDQ+∠QDC=180度、
3θ+4θ+2θ=180度、
よって、θ=180度/9=20度。∠BAC=100度は解答例1と同様。
解答例3(MrXさん、他)
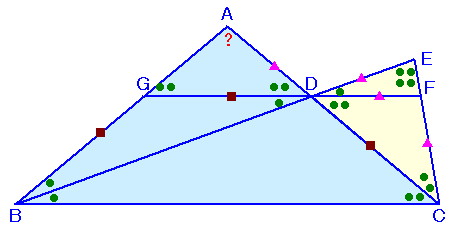
BDを延長し、DE=ADとなる点をEとし、
Dを通りBCと平行に引いた直線とECの交点をF、ABとの交点をGとします。
また、∠ABD=∠DBC=θとします。
△AGDは△ABCと相似な二等辺三角形、
よって、∠AGD=∠ADG=2θ。GDとBCは平行より、∠GDB=∠DBC=∠GBD=θ、
よって、△GBDはGB=GDの二等辺三角形。BE=BD+BE=BD+AD=BC、
よって、△BCEはBE=BCの二等辺三角形、
従って、∠BEC=∠BCE。DFとBCが平行より、∠DFE=∠BCE=∠DEF、
よって、△DEFはDE=DFの二等辺三角形。また、GDとBCは平行より、GB=DC。
さて、△ADGと△FDCについて、
AD=FD、DG=DC、∠ADG=∠FDC=2θより二辺挟角が等しいので合同。
よって、△FDCもFD=FCの二等辺三角形。従って、∠FCD=∠FDC=2θ。
△BCEは二等辺三角形であったから、∠BEC=∠BCE=4θ。よって、△BCEの内角の和=9θ=180度。
従って、θ=20度。
以下同様。
(その他の解法)
・作図して求める ・・・
ミミズクはくず耳さん 、M.Hossieさん 、中村明海さん・数値計算で三角方程式を解く ・・・ ハラギャーテイさん 、小西孝一さん
・座標を用いて方程式を解く ・・・ ハラギャーテイさん 、拓パパさん