第２９５問の解答

問題　［規則性］

問題図

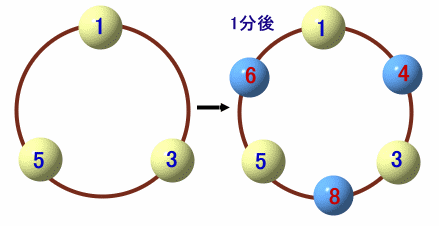
上の図のように、円周上に１、３、５の数字が書かれています。

この図は、１分後には右側の図のように、数字と数字の間に新たな数字が書き足されます。このとき、新たな数字は、その両側の数字の合計になっています。上の図（右側）だと、１と３の間に４、３と５の間に８、５と１の間に６が書かれていますね。

このようにして１分ごとに数字を書き足していくとき、
（１）　４分後、円周上にある数字の合計はいくつになるでしょうか。

（２）　７分後、円周上にある数字の中で最大のものはいくつでしょうか。

　

解答例１（Mikiさん、トトロ＠Ｎさん、Masashiさん、あんみつさん、ねこやんさん、拓パパさん、小西孝一さん、前田先生＠P進学院さん、M.Hossieさん、あまれっとさん、tekiさん、有無相生さん、大岡敏幸さん、永井暁さん、他多数）

n分後の数字の合計をFn、最大の数字をGnとし、漸化式で考えます。

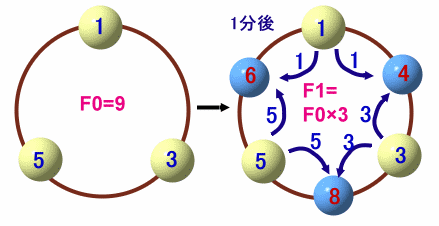
（１）数字の合計

参考図１

(n-1)分後と、n分後の数字を比べてみます。
n分後には、
　・(n-1)分後の数字がそのまま残ったもの
　・(n-1)分後の数字を左、右の両隣に加えたもの
の合計だから、
　Fn＝Fn-1＋Fn-1×２＝Fn-1×３

従って、Fnは、初項がF0=９で、公比が３の等比数列となります。
よって、Fn＝９×３n＝３n+2、４分後はF4＝３6＝７２９となります。

（２）数字の最大値

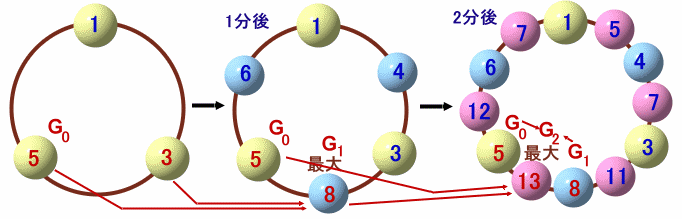
n=２のときを考えます。

参考図２

２分後に新しく書き込まれる数字（上図、ピンクの球）は、
最初にあった数字（黄色の球）と１分後に書き込まれた数字（青い球）の和となっています。

黄色の球の最大値G0＝５と青色の球の最大値G1＝８は隣り合っているので、ピンク色の球の最大値G2＝G0＋G1＝５＋８＝１３となります。

そして、G2とG1が今度も隣り合うことになるので、３分後も同様にして、
　G3＝G1＋G2＝８＋１３＝２１

以下、同様にして、　Gn＝Gn-1＋Gn-2
が成り立つので、Gnはフィボナッチ数列となります。
順次計算して求めると、G7＝１４４となります。

参考図３
　

答：（１）７２９　（２）１４４

以上

（その他の解法）

・EXCELなどを用いて地道に計算して求める・・・
　　圭太さん 、角田(^^)v鉄也さん 、ちーくんさん 、takuさん 、カズノリさん 、masaki_satouさん 、他