第２９７問の解答

問題　［平面図形］

問題図

左図のような、底面が一辺６cmの正方形、高さが９cmで、側面がすべて合同な二等辺三角形でできた正四角錐Ａ−ＢＣＤＥがあります。

まず、この正四角錐を平面ＡＢＤ、平面ＡＣＥで切断し、次に、この正四角錐を図のような平面ＢＰＱＲで切断します。このとき、ＡＱ：ＱＤ＝１：１となっています。

その結果、正四角錐は８つの立体に分割されますが、その中から形が三角錐（四面体）であるもの４つの体積を測ったところ、その比は２：３：４：６でした。

では、上図の正四角錐Ａ−ＢＰＱＲの体積は何cm3でしょうか。

解答例１（Taroさん、小杉原啓さん、トトロ＠Ｎさん、ＩＣさん、真島嘉弘TZさん、おかひで博士さん、CRYING DOLPHINさん、有無相生さん、小西孝一さん、ふじさきたつみさん、ねこやんさん、ミミズクはくず耳さん、トモさん、圭太さん、あさみかずみさん、 他多数）

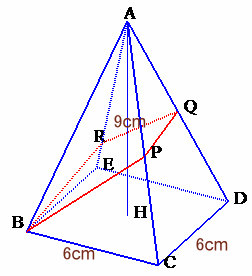
Aから底面BCDEに下ろした垂線の足をHとし、PRとBQの交点をTとします。
また、AP<ARと仮定しても一般性を失いません。。

参考図１

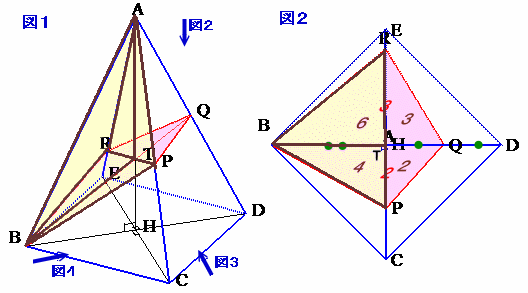
対象性より、Hは正方形BCDEの中心、AHが正四角錐の高さとなります。
また、Tは３つの平面ACE、ABD、BPQRの上にあるので、AHとBPQRの交点となります。

図１より、問題にある４つの三角錐とは、正四角錐を平面BPQRで切断した上側、A-TRB、A-TBP、A-TPQ、A-TQRとなります。

これらは、底面が全て平面BPQRにあり、高さ（AからBPQRに下ろした垂線）が共通なので、体積は底面の面積に比例します。

図１、図２より、△TRB：△TRQ＝△TPB：△TPQ＝２：１、また仮定より、△TRB＞△TQBなので、題意より、
　△TPQ：△TRQ：△TPB：△TRB＝２：３：４：６と分かります。

さて、平面ABDとACEは直交しているので、三角錐A-RBPは、底面を△ARPと考えると、高さはBHに等しくなるので、
　三角錐A-RBP：三角錐A-EBC＝△ARP：△AECとなります。　・・・（１）

参考図２

また、図３から、Tは二等辺三角形ABDの重心となるので、
　AT：TH=２：１となります。

さて、図４でPからAHに下ろした垂線の足をP'とし、RからAHに下ろした垂線の足をR'とします。

　三角錐A-TRB：三角錐A-TBP＝△ATR：△ATQ＝RR'：PP'＝３：２。

よって、P'T＝２とおくと、△TRR'と△TPP'が相似より、
　TR'＝P'T×RR'/PP'＝２×３/２＝３となります。

また、∠EAH＝∠CAHなので、△ARR'と△APP'は相似、
よって、AR'：AP'＝RR'：PP'＝３：２、従ってAP'＝P'R'×２＝５×２＝１０。

よって、AT＝AP'＋P'T＝１０＋２＝１２。
ところが、AT：TH＝２：１なので、TH＝１２×1/2＝６、
よってR'H＝TH−TR'＝６−３＝３。

△ARR'、△AEH、△APP'、△ACHは全て相似、
よって、AR：AE＝AR'：AH＝１５：１８＝５：６、AP：AC＝AP'：AH＝１０：１８＝５：９。

従って、（１）より、
　三角錐A-RBP
＝三角錐A-EBC×△ARP/△AEC
＝1/3×（６2×1/2）×９×5/6×5/9
＝２５cm3

よって、正四角錐Ａ−ＢＰＱＲ
＝三角錐A-RBP＋三角錐A-PQR
＝２５＋２５×1/2
＝７５/２cm3

（参考）マウスでドラッグして下さい。

答：75/2cm3

以上

（その他の解法）