第２９８問の解答

問題　［平面図形］

問題図

左図のような、一辺の長さが７cmの正方形ＡＢＣＤがあります。

点Ｐを辺ＡＤ上にＡＰ＝２cmとなる位置に、点Ｑを辺ＣＤ上に∠ＡＰＢ＝∠ＱＰＢとなるようにします。
また、点Ｑを通りＢＰに平行な直線と辺ＢＣとの交点をＲとします。

このとき、ＤＱの長さは何cmでしょうか。
　

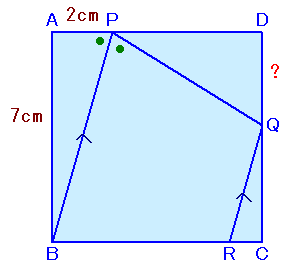解答例１

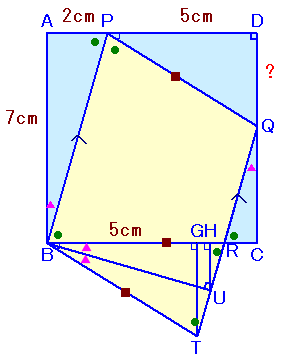
RQとＡＤの延長線の交点をTとします。
また、∠ＴＰＱの二等分線とＱＴの交点をＧとし、ＧからＤＴに下ろした垂線の足をＨとします。

参考図１

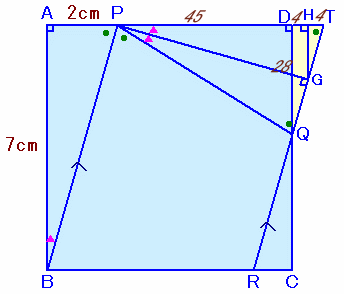
ＰＢとＴＲは平行だから、∠ＰＴＧ＝∠ＡＰＢ＝∠ＢＰＱ＝∠ＰＱG。
よって、△ＰＱＴはＰＴ＝ＰＱの二等辺三角形。

従って、ＧはＱＴの中点となり、ＰＧとＱＴは直交します。
また、ＨはＤＴの中点となります。

△ＴＧＰ、△ＴＨＧ、△ＧＨＰは△ＰＡＢと相似。

よって、ＨＴの長さを４とすると、
　ＨＧ＝ＨＴ×７／２＝１４、ＰＨ＝ＨＧ×７／２＝４９。
ＤＧ＝ＨＴ＝４だから、ＰＤ＝ＰＨ−ＤＨ＝４９−４＝４５。

また、ＤＱ＝ＨＧ×２＝２８。

従って、ＤＱ＝ＰＤ×２８／４５＝５×２８／４５＝２８／９cm。

（類似解）

maruhagedonさん

PBTQは平行四辺形とし、TからBCに下ろした垂線の足をGとします。

参考図２

△BGTと△PDQは合同より、BG=５ｃｍ、GT＝DQ。
あとは解答例１と同様にしてGT＝２８／９ｃｍを得ます。

　

辻さん

PTRQを平行四辺形とし、TからBCに下ろした垂線の足をHとします。

参考図３

△THRと△QDPは合同より、HR＝PD＝５ｃｍ、TH＝DQ。
以下同様。

答：28/9cm

以上

解答例２（トトロ＠Ｎさん、Banyanyanさん、ちーくんさん、他）

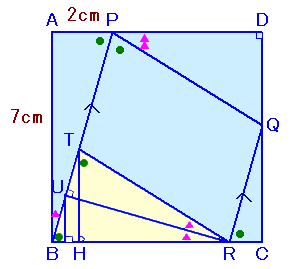
PBを軸にして△PABを折り返したものを△PA'Bとします。
A'からAB、AD、BCに下ろした垂線の足をそれぞれH、H'、H2とし、
AA'とPBの交点をTとします。

参考図4


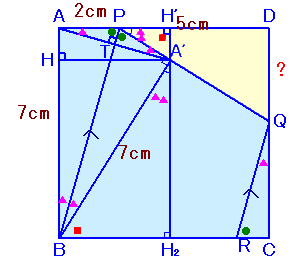
ピタゴラスの定理より、PB2＝AP2＋AB2＝２2＋７2＝５３、
よって、PB＝√53。

△PTAと△PTA'は合同で、△PABに相似、
よって、AT＝A'T＝２×７／√53＝１４／√53。

△A'H'Aも△PABに相似、
よって、
　AH'＝AA'×７／√53＝２×１４／√53×７／√53＝１９６／５３、
　A'H'＝AA'×２／√53＝２×１４／√53×２／√53＝５６／５３。

PH'＝AH'−AP＝１９６／５３−２＝（１９６−１０６）／５３＝９０／５３。

△PH'A'と△PDQは相似だから、
DQ＝PD×AH'／PH'＝５×５６／９０＝２８／９ｃｍ。

　

（別解）

AH'＝ｘとおきます。
△PA'H'と△A'BH2は相似だから、
　　BH2＝A'B×A'H'／PA'＝７×ｘ／２＝7/2ｘ、
　　PH'＝PA'×A'H2／A'B＝２×（７−ｘ）／７＝２−2/7ｘ.。

AH'＝BH2だから、
　２＋（２−2/7ｘ.）＝7/2ｘ
　（2/7+7/2）x＝４
よって、ｘ＝５６／５３。
PH'＝２−2/7ｘ.＝９０／５３。

以下同様。

解答例３（ふじさきたつみさん、 他）

PBを軸にして△PABを折り返したものを△PA'Bとし、DQ＝ｘとおきます。
　

参考図５

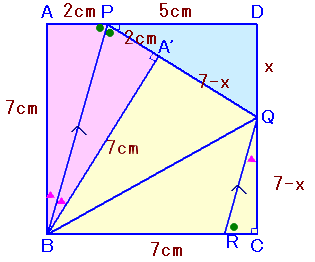
A'B＝AB＝BC＝7cmなので、直角三角形QBA'とQBCは合同。
（A'Q2＝BQ2−A'B2＝BQ2−BC2＝QC2）

従って、
　正方形ABCD＝△PAB×２＋△QBC×２＋△PDQ
　４９＝１４＋７×（７−ｘ）＋５/２ｘ
　９/２ｘ＝１４
よって、ｘ＝２８/９ｃｍとなります。

（類似解）

sodoさん、うのたかはるさん 、有無相生さん

PからBCに下ろした垂線の足をHとし、PHとBQの交点をTとします。

参考図６

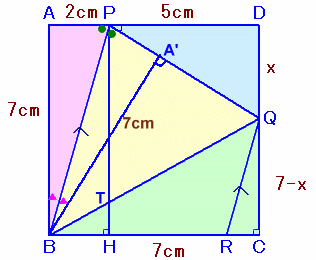
正方形ABCD＝△PAB＋△PBQ＋△QBC＋△PDQ
　４９＝1/2×２×７＋1/2×５×√（５2＋ｘ2）×７＋1/2×（７−ｘ）×７＋1/2×５×ｘ
変形して、９ｘ2−２８ｘ＝０。

これより、ｘ＝２８/９を得ます。

解答例４（ねこやんさん、 他）

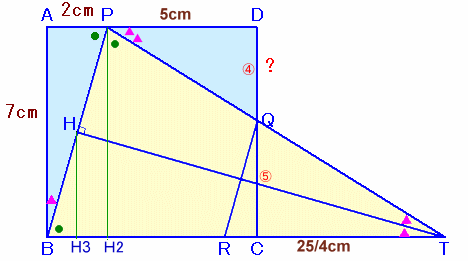
PQとBCの延長が交わる点をTとし、TからPBに下ろした垂線の足をHとします。

参考図７

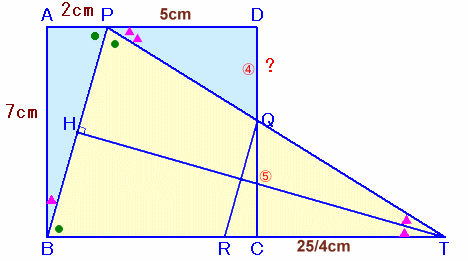
ピタゴラスの定理より、ＰＢ＝√53。

△TPHと△TBHは、ともに△BPAと相似、かつTHは共通だから合同。
よって、BT＝ＨB×√53/2＝(√53/2)2＝５３／４。

従って、ＣＴ＝ＢＴ−ＢＣ＝５３／４−７＝２５／４。

△ＤＰＱと△ＣＴＱは相似で、相似比はＤＰ：ＣＴ＝５：２５/４＝４：５。
よって、ＤＱ＝ＣＤ×４／９＝７×４／９＝２８／９ｃｍ。


　

（類似解）

ちば けいすけさん、あんみつさん

Ｐ、ＨからＢＣに下ろした垂線の足をＨ2、Ｈ3とします。

参考図８

△ＰＢＨ2で中点連結定理より、
　ＢＨ3＝Ｈ3H2＝1ｃｍで、HＨ3＝７／２ｃｍ。

△ＴＨＨ3と△ＢＰＡは相似だから、
　Ｈ3Ｔ＝ＨＨ3×７／２＝４９／４ｃｍ。

よって、ＢＴ＝ＢＨ3＋Ｈ3Ｔ＝１＋４９／４＝５３／４ｃｍ。
以下同様。

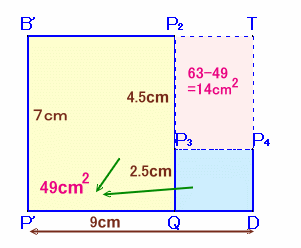
解答例５（まるケンさん、 他）

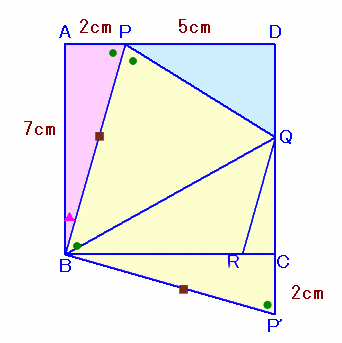
Ｂを中心に△ＡＰＢを時計方向に９０度回転したものを△Ｐ'ＣＢとします。

参考図９ 参考図９−１

△ＰＢＱと△Ｐ'ＢＱは、ＰＢ＝Ｐ'Ｂ、ＢＱは共通で∠ＢＰＱ＝∠ＢＰ'Ｑ。
よって、右の図のようにＰ'は三点ＰＢＣを通る円周上、および点Ｂを中心とし半径がＰＢに等しい円周上にあることになる。

このような点はＰを含め２カ所あるが、もう一方の∠ＢＰ'Ｑは∠ＢＰＱとは等しくないので、結局Ｐ以外にはないことになる。

よって、△ＰＢＱと△Ｐ'ＢＱは合同。

従って、面積について、
　正方形ＡＢＣＤ＝△ＰＢＱ＋△Ｐ'ＢＱ＋△ＰＱＤ

三角形だとわかりにくいので、△ＰＢＱと△Ｐ'ＢＱはくっつけて変形し、ＱＰ'（＝ＱＣ＋２ｃｍ）を底辺、高さ７の長方 形に、また、△ＰＱＤも、底辺がＤＱ、高さが半分の２．５ｃｍの長方形にします。

参考図９−２

すると、
　長方形Ｐ2Ｐ3Ｐ4Ｔ
＝長方形Ｂ'Ｐ'ＤＴ−（長方形Ｂ'Ｐ'ＱＰ2＋長方形Ｐ3ＱＤＰ4）
＝７×９−４９＝１４ｃｍ2。

よって、QD＝１４÷（７−２．５）＝２８／９ｃｍ2。

解答例６（CRYING DOLPHINさん、うっしーさん他）

DQ＝ｘとおきます。

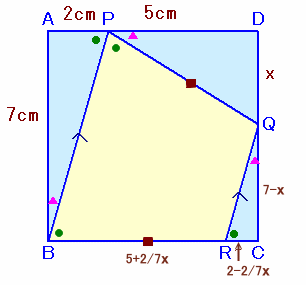
参考図１０

QC＝CD−DQ＝７−ｘ。

△QRCは△BPAと相似だから、
　RC＝QC×２/７＝２−２/７ｘ。
よって、BR＝BC−RC＝５＋２/７ｘ。

四辺形QPBRは、等脚台形になるからPQ＝BR。

△PDQでピタゴラスの定理により、
　PD2＋DQ2＝PQ2、
　５2＋ｘ2＝（５＋２/７ｘ）2、
　２５＋ｘ2＝２５＋２０/７ｘ＋４/４９ｘ2、
　４９ｘ2＝１４０ｘ＋４ｘ2、
　ｘ（４５ｘ−１４０）＝０
ｘ＞０だから、ｘ＝１４０/４５＝２８/９ｃｍ。

解答例８（Taroさん、Miki Sugimotoさん、ハラギャーテイさん、M.Hossieさん、ばち丸さん、 他）

α＝∠APB＝∠BPQ、θ＝∠DPQとおきます。

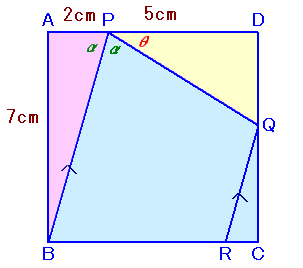
参考図１２

直角三角形BPAより、tanα＝７/２。
θ＝１８０度−２αより、
tanθ＝−tan２α＝−２tanα／（１−tan2α）＝−２・７/２／（１−７2/２2）＝２８/４５。

ＤＱ＝ＰＤ・tanθ＝５・２８/４５＝２８/９。