第299問の解答
問題 [速さの問題]
|
マサルさんは、あるデパートの下りエスカレータに乗って歩いています。
マサルさんは財布を落としたのに気づくとすぐに方向転換し、歩いてエスカレータを上りはじめました。その後マサルさんは財布を拾うと下に向かって歩き始め、財布を拾ってから21段歩いたところで下の階に着いたそうです。 |
解答例1(ねこやんさん、トトロ@Nさん、Taroさん、M.Hossieさん、有無相生さん、他)
財布を落とした時刻をT1、財布を落としたことに気づいた時刻をT2、
財布を拾った時刻をT3、下の階に着いた時刻をT4とします。
また、マサルさん、およびエスカレータの速さをv1、v0とします。
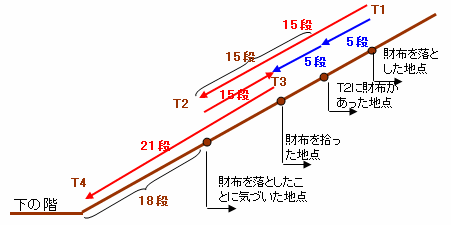
T1からT2にかけて、
マサルさんが実際に下りる速さは、v1+v0、財布の速さはv0なので、速度差はマサルさんの速度v0に等しい。
よって、マサルさんと財布の距離はちょうど15段になります。T2からT3にかけて、
マサルさんが上がる実際の速さは、v1−v0、財布の下りる速さはv0なので、速度和はマサルさんの速度v0に等しい。よって、マサルさんが15段上がったつもりで、ちょうど財布と出会います。T2からT4にかけて、
マサルさんは、15段上がって21段下がるので、もしエスカレータが止まっていたとしたら21−15=6段下がった地点、すなわち下の階から18−6=12段の地点にいることになります。ということは、この間にエスカレータが進むのは、この12段分であり、マサルさんは15+21=36段だけ進んだことになるので、両者の速度比は36:12=3:1と分かります。
T1からT2にかけて、財布の下りた段数はマサルさんの進んだ15段×1/3=5段、
よって、最初に財布を落とした地点は下の階から18+15+5=38段目になります。マサルさんが上るときの実際の速さは、v1−v0=v1-1/3×v1=2/3×v1、
よって、実際に38段上がるためには、38×3/2=57段進む必要があります。答:57段
以上
解答例2(CRYING DOLPHINさん、ちば けいすけさん、他)
エスカレータが止まっていて、替わりに下の階がエスカレータの速度分上がってくると考えたダイアグラムを書きます。
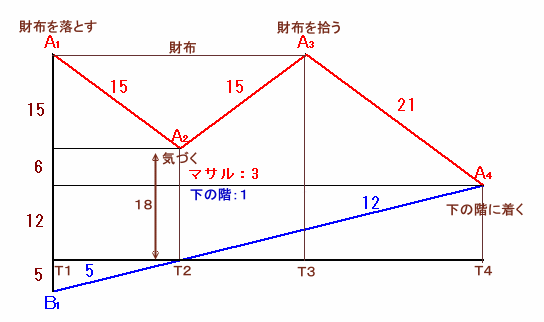
T2からT3にかけて、マサルさんが引き返して財布を拾うには、下りたと同じ15段進みます。
T2からT4にかけて、マサルさんは、15段上がって21段下がるので、21−15=6段下がります。
すると、下の階は気づいた地点から18−6=12段上がったことになります。この間、マサルさんは25+21=36段進み、下の階は12段進むので、両者の速度比は3:1。
よって、T1からT2にかけて下の階は、15×1/3=5段だけ進んだことになります。
従って、T1で財布と下の階の距離は5+18+15=38段あったことになります。以下同様。
(その他の解法)
方程式で解く・・・ミミズクはくず耳さん、 他