第３００問の解答

---

問題　［ 空間図形］

左図のような各面が平行四辺形からなる平行六面体ＡＢＣＤ-ＥＦＧＨがあります。 今、底面上の点Ｐを△ＥＦＨの内部にとり、ＤＰ上の点Ｑをとったとき、次の関係が成り立ちました。 四角錐Ｑ-ＡＢＣＤの体積＝７２cm3 四角錐Ｑ-ＡＥＨＤの体積＋四角錐Ｑ-ＣＤＨＧの体積＝６０cm3 三角錐Ｑ-ＤＦＧの体積＝３０cm3 平行四辺形ＥＦＧＨの面積＝７２cm2 では、△ＰＦＨの面積は何cm2でしょうか。

---

解答例１（マサルさん 、ねこやんさん、おかひで博士さん、Banyanyanさん、ミミズクはくず耳さん、水田Xさん、他）

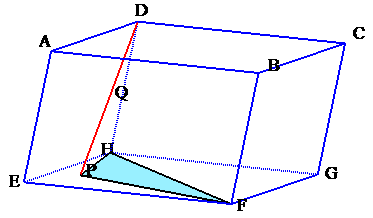
（動く３Ｄ図）

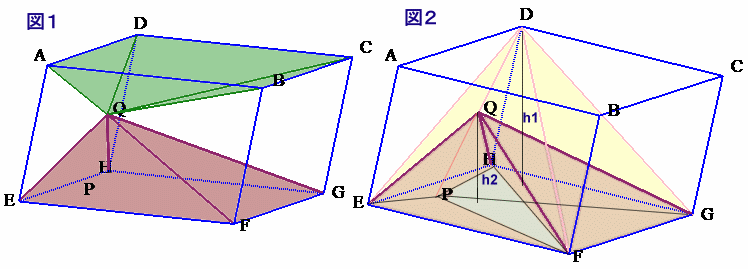
図１、図２より、
　四角錐Ｄ-ＥＦＧＨ＝四角錐Ｑ-ＡＢＣＤ＋四角錐Ｑ-ＥＦＧＨ＝平行六面体×1/3　・・・　（１）
　四角錐Ｄ-ＥＦＧＨ＝三角錐Ｑ-ＤＥＦ＋三角錐Ｑ-ＤＦＧ＋三角錐Ｑ-ＤＧＨ＋三角錐Ｑ-ＤＨＥ
　　　　　　　　　　　　　＋四角錐Ｄ-ＥＦＧＨ　・・・　（２）
が成り立ちます。

（１）より、
　四角錐Ｄ-ＥＦＧＨ＝７２＋四角錐Ｑ-ＥＦＧＨ

また、
　三角錐Ｑ-ＤＧＨ＋三角錐Ｑ-ＤＨＥ
＝四角錐Ｑ-ＡＥＨＤ×1/2＋四角錐Ｑ-ＣＤＨＧの体積×1/2
＝６０×1/2＝３０cm³
および、三角錐Ｑ-ＤＦＧ＝３０cm³だから、
（２）より、
　７２＋四角錐Ｑ-ＥＦＧＨ＝３０＋３０＋三角錐Ｑ-ＤＥＦ＋四角錐Ｑ-ＥＦＧＨ

よって、
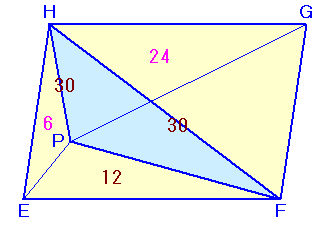
　三角錐Ｑ-ＤＥＦ＝７２−６０＝１２cm³。

さて、平面ＥＦＧＨから見た点Ｄの高さをh1、点Ｑの高さをh2とします。

すると、
　三角錐Ｑ-ＤＥＦ＝三角錐Ｄ-ＰＥＦ−三角錐Ｑ-ＰＥＦ＝△ＰＥＦ×(h1-h2)×1/3
　三角錐Ｑ-ＤＦＧ＝三角錐Ｄ-ＰＦＧ−三角錐Ｑ-ＰＦ Ｇ＝△ＰＦＧ×(h1-h2)×1/3
　三角錐Ｑ-ＤＧＨ＋三角錐Ｑ-ＤＨＥ
＝（三角錐Ｄ-ＰＧＨ−三角錐Ｑ-ＰＧＨ）＋（三角錐Ｄ-Ｐ ＨＥ−三角錐Ｑ-ＰＨＥ）
＝（△ＰＧＨ＋△ＰＨＥ）×(h1-h2)×1/3

また、
　三角錐Ｑ-ＤＥＦ＋三角錐Ｑ-ＤＦ Ｇ＋三角錐Ｑ-ＤＧＨ＋三角錐Ｑ-ＤＨＥ
＝四角錐Ｄ-ＥＦＧＨ−四角錐Ｑ-ＥＦＧＨ
＝平行四辺形ＥＦＧＨ×(h1-h2)×1/3
＝四角錐Ｑ-ＡＢＣＤ
＝７２cm³。

従って、
　三角錐Ｑ-ＤＧＨ＋三角錐Ｑ-ＤＨＥ＝７２−（１２＋３０）＝３０cm³。

よって、
　△ＰＥＦ：△ＰＦＧ：（△ＰＧＨ＋△ＰＨＥ）
＝三角錐Ｑ-ＤＥＦ：三角錐Ｑ-ＤＦＧ：三角錐Ｑ-ＤＧＨ＋三角錐Ｑ-ＤＨＥ
＝１２：３０：３０。

従って、
　△ＰＥＦ＝１２cm²、△ＰＦＧ＝３０cm²、（△ＰＧＨ＋△ＰＨＥ）＝３０cm²。

△ＰＥＦ＋△ＰＧＨ＝△ＰＦＧ＋△ＰＨＥ＝平行四辺形ＥＦＧＨ×1/2＝７２×1/2＝３６cm²。

よって、
　△ＰＧＨ＝３６−１２＝２４cm²。

従って、
　△ＰＦＨ＝△ＰＦＧ＋△ＰＧＨ−△ＦＧＨ
＝３０＋２４−３６
＝１８cm²。

答：１８cm²

以上

---

（その他の解法）

• 座標、ベクトルで解く・・・Taroさん、Toru Fukatsuさん、M.Hossieさん、他

---