第301問の解答
問題 [推理]
|
|
|
|
|
|
ある学校の生徒に次のようなアンケート調査をしました。 質問:「あなたの好きなスポーツを2つ書いてください。」 その結果、80枚のアンケート用紙が集まり、どのアンケート用紙にも2種類のスポーツが書いてあったそうです。 また、この80枚のアンケート用紙から適当に2枚を選び、そこに書かれたスポーツを見ると、どのように2枚を選んでも、必ず2枚に共通するスポーツが少なくとも1つあったそうです。 では、生徒に最も好まれたスポーツは、少なくとも何枚のアンケート用紙に書かれていたと考えられるでしょうか。 |
|
|
|
|
|
解答例1
| ミミズクはくず耳さん 、Taroさん、ねこやんさん、中村明海さん、M.Hossieさん、有無相生さん、水田Xさん、小西孝一さん、nobさん、ふじさきたつみさん、ばち丸さん、Parpunteさん、あまれっとさん、トトロ@Nさん、長野美光さん、巷の夢さん、N.Nishiさん、他 |
アンケートに記入されたスポーツの種類数によって場合分けします。
スポーツが2種類のとき
全ての生徒がこの2種類のスポーツを書いたことになり、どちらも80枚に記入されています。
スポーツが3種類のとき
3種類のスポーツを記入数の多い順に、A、B、Cとし、記入数をそれぞれ、a、b、c枚とします。
題意より、
a+b+c=80×2=160
a≧b≧c
が成り立つので、
a×3≧160
a≧160/3=53.33・・・従って、a≧54。
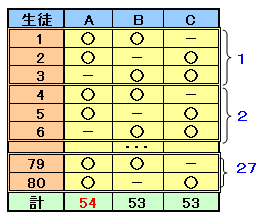
実際、下表のような組み合わせが存在するので、最も好まれたスポーツの記入数は、少なくとも54枚以上。
スポーツが4種類以上のとき。
最も好まれたスポーツをAとします。
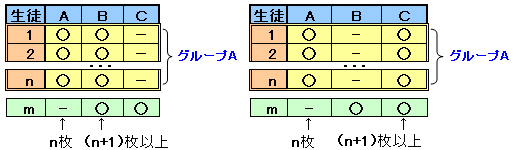
このとき、実は全員がAを記入したことになりますが、これを背理法で証明します。今、Aを記入した人(n人:ただし、n<80)ばかりを集めてグループAということにします。
グループA以外の人が少なくとも一人(生徒mと呼びます)存在するので、この人が記入したスポーツをB、Cとします。
題意より、グループAのそれぞれと生徒mは、同じスポーツを一つは記入していますが、それはAではないのでBまたはCを記入していることになります。
もし、グループAの全員がA、Bと記入したと仮定すると、スポーツBを記入した人が(n+1)以上いることになり矛盾します。グループAの全員がA、Cと記入したと仮定しても同様。
従って、グループAには、A、Bと記入した人、A、Cと記入した人の両方が存在します。
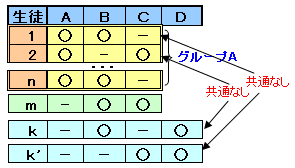
さて、仮定から記入されたスポーツは4種類以上なので、A、B、C以外のスポーツ(Dとします)を記入した人(生徒kと呼びます)が存在します。
生徒kは生徒mと共通なスポーツを一つは記入しているので、Dの他にBまたはCを記入しています。
生徒kがB、Dとすると、グループAでA、Cを記入した生徒2と共通なスポーツがないので矛盾。
生徒kがC、Dとすると、グループAでA、Bを記入した生徒1と共通なスポーツがないので矛盾。従って、いずれの場合も矛盾が生じるので、グループAに属さない人がいるという仮定が誤っていたことになります。
よって、全員がスポーツAを記入したことになるので、最も好まれたスポーツAの記入数は80枚となります。
以上から、最も好まれたスポーツの記入数の最小値は54枚と分かります。
答:54枚
以上