第302問の解答
問題 [ 平面図形]
|
|
|
|
|
|
|
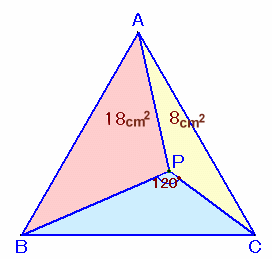 |
左図のような正三角形ABCがあります。 いま、その内部に∠BPC=120度となるような点Pをとったところ、△APBの面積が18cm2、△APCの面積が8cm2となりました。 では、この正三角形ABCの面積は何cm2でしょうか。 |
|
|
|
|
|
|
解答例1
sugitakukunさん 、chiocciolaさん、マサルさん、ヒデー王子さん、CRYING DOLPHINさん、拓パパさん、M.Hossieさん、水田Xさん、 他
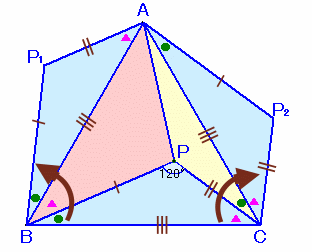
Bを中心に△PBCを反時計回りに60度回転したものを△P1BA、
Cを中心に△PBCを時計回りに60度回転したものを△P2ACとします。
題意より、
∠PBC+∠PCB=180−∠BPC=180−120=60度。従って、
∠ABP=∠P1AB=∠PCB、
∠ACP=∠P2AC=∠PBC。すると、P1AとBPは平行なので△APBと△AP1Bは高さが等しくなり、面積比は底辺の比に等しい。
よって、△APB:△AP1B=18:△PBC=PB:P1A=PB:PC ・・・ (1)同様に、△P2AC:△APC=△PBC:8=AP2:PC=PB:PC ・・・ (2)
(1)、(2)より、
18:△PBC=△PBC:8
△PBC2=18×8=144よって、△PBC=12cm2となり、
正三角形ABC=18+8+12=38cm2となります。
答:38cm2
以上
解答例2
ちば けいすけさん、 他
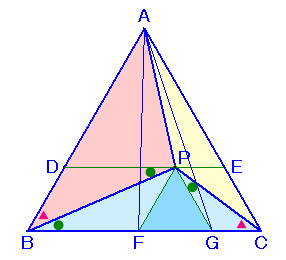
Pを通ってBCに平行な直線を引き、AB、BCとの交点をそれぞれD、Eとする。
また、BC上に、Bに近い方から2点F、Gをとり、△PFGが正三角形になるようにする。
すると、二つの平行四辺形BDPFとCFPGとができる。
△APB=△AFB、△APC=△AGC。
よって、BF:CG=△APB:△APC=18:8=9:4。一方、∠DBP=∠GCP、∠BDP=∠CGPより、△DPB∽△GPC。
BF:CG=9:4より、DP:GP=9:4。したがって、△DPB:△GPC=9:4。
相似で面積比が9:4だから、DP:GP=3:2。
従って、BF:FG:GC=9:6:4。
よって、△ABC=18+8+18×6/9=38cm2。
解答例3
トトロ@Nさん、 他
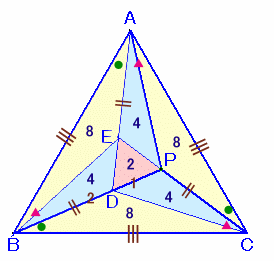
PB上に点DをBD=PCとなるようにとり、ADとCPの延長線の交点をEとします。
△DBCと△PCAは二辺挟角が等しいので合同。
△ABDと△PBCは二辺挟角が等しいので合同。従って、∠BAD=∠PBC、∠DAC=60−∠BAD=60−∠PBC=∠PCB。
すると、△PBCと△ECAは、1辺と両端の角が等しいので合同。
以上から、AE=BD=PC、AD=EC=PB、
よって、ED=AD-AE=PB−PC=PD、EP=EC−PC=PB−PC=PD。ここで、PD/BD=xとおくと、
△DBC=△ABE=△APC=8cm2。
△PDC=△DEB=△EPA=8x cm2。
△EDP=△EPA・x=8x2 cm2。従って、△APC=8+2・8x+8x2=18
4x2+8x−5=0
(2x−1)(2x+5)=0
よって、x=1/2となります。従って、
△ABC=8・3+8・1/2・3+8×1/2・1/2=24+12+2=38cm2。
(その他の解法)
Pから各辺に垂線を下ろして相似形を利用 ・・・ maruhagedonさん、ねこやんさん、他
三角関数で解く ・・・ 有無相生さん、モルモット大臣さん、他
ベクトルで解く ・・・ ハラギャーテイさん、 他