第３０３問の解答

問題　［場合の数］

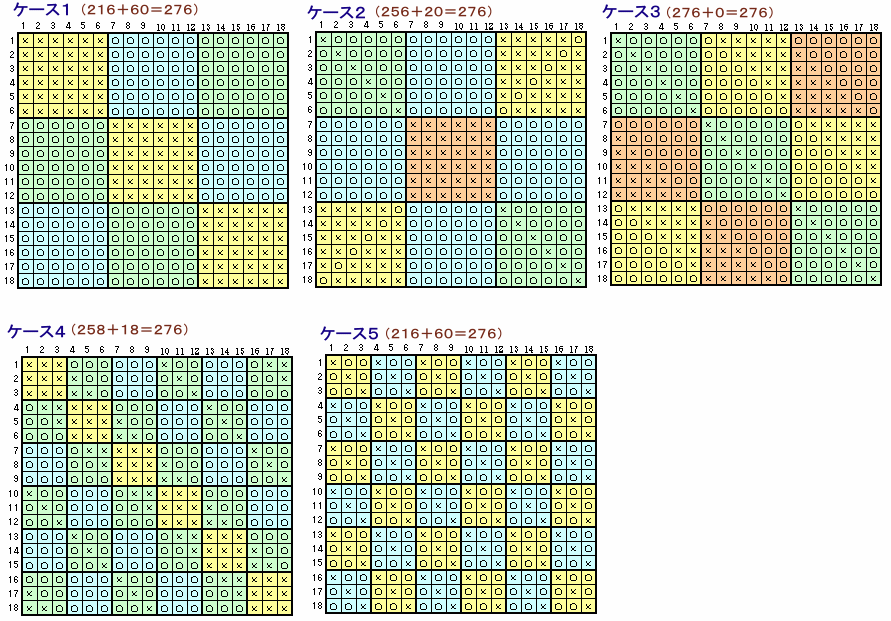
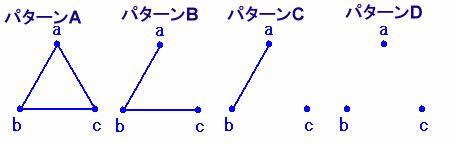
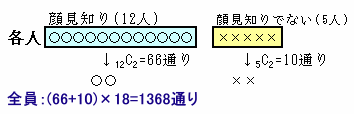
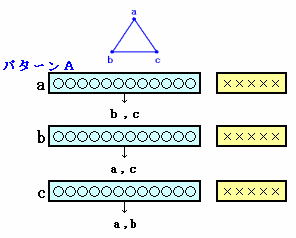
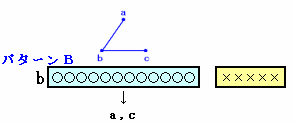
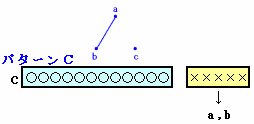
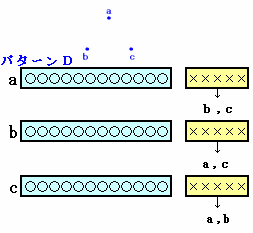
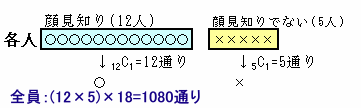
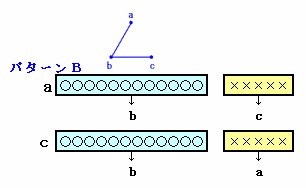
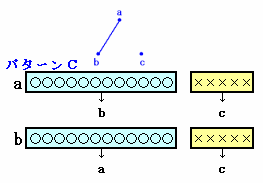
ある小学校では４月に「クラス換え」が行われました。
６年１組は１８人学級になりましたが、そのクラスで「顔見知りだった人は何人いましたか？」という質問をしたところ、全員が１２人と答えたそうです。

では、６年１組の１８人の中から３人を選びだすとき、３人とも互いに顔見知りか３人とも互いに知り合いでないのどちらかの条件にあてはまるような選び方は何通りありますか。

解答例１

１８人のそれぞれが顔見知りが１２人という条件を満たす例を下表のようなマトリクスで考えます。
ここで、○は互いに顔見知り、×は互いに知り合いでないことを表します。

いずれのケースも、３人とも互いに顔見知りか３人とも互いに知り合いでない場合は、２７６通りとなっていますので、２７６通りが答と想像できます。

  • ケース１・・・トトロ＠Ｎさん 、Taroさん、 とのさん、ＩＣさん、ミミズクはくず耳さん、きょえぴさん、あんみつさん、あさみかずみさん、 他
  • ケース２・・・有無相生さん、 他
  • ケース３・・・ごんごんまさん、manabuさん、 他
  • ケース４・・・中村明海さん 他
  • ケース５・・・ねこやんさん、 他　

なお、この考え方では、全てのケースで２７６通りであるかどうかは分かりませんので解答としては、不充分です。

答：２７６通り

以上

解答例２

マサルさん

１８人の中から３人を選ぶ方法は、全部で18C3＝８１６通りあります。 （方法１）
ここでは、各人を点で表し、線分は２人が顔見知りのときを表しています。

参考図２

これらを上記４パターンに分類します。

  • パターンA　・・・　３組のペアとも顔見知り

  • パターンB　・・・　２組のペアは顔見知り、１組のペアは顔見知りでない

  • パターンC　・・・　１組のペアは顔見知り、２組のペアは顔見知りでない

  • パターンD　・・・　顔見知りのペアはない

本問では、パターンＡおよびパターンＤの場合の数の合計を求めることになります。

さて、各人が自分の顔見知りから２人または顔見知りでない人から２人選ぶ選び方を考えます。（方法２）

参考図３

方法２では、ある特定の人から見て、

  • 自分の顔見知りから２人を選ぶ方法：　　12C2＝６６通り

  • 自分の顔見知りでない２人を選ぶ方法：　5C2＝１０通り

 合計６６＋１０＝７６通り、従って全員では、７６×１８＝１３６８通りとなります。

ここで、方法１の選び方４パターンと方法２の選び方との関連を考えます。

１８人の中から任意の３人を選び、ａ、ｂ、ｃとします。

  • パターンAのとき　・・・　
    方法２では、ａ、ｂ、ｃそれぞれが、残り２人を顔見知りとして選ぶので、
    同じ組み合わせを合計３回数えることになる。
    　参考図３−１
    　

  • パターンＢのとき　・・・　ｂがａ、ｃと顔見知りとします　
    方法２では、ｂが、残り２人を顔見知りとして選ぶだけなので、
    同じ組み合わせ    は１回だけ数えることになる。
    　参考図３−２
    　

  • パターンＣのとき　・・・　ａとｂが顔見知りとします　
    方法２では、ｃが、残り２人を顔見知りでないときにだけ選ぶので、
    同じ組み合わせ    は１回だけ数えることになる。
    　参考図３−３
    　

  • パターンＤのとき　・・・　
    方法２では、ａ、ｂ、ｃそれぞれが、残り２人を顔見知りでないとして選ぶので、
    同じ組み合わせを合計３回数えることになる。
    　参考図３−４

従って、パターンＡ、Ｂ、Ｃ、Ｄの場合の数をそれぞれＡ、Ｂ、Ｃ、Ｄとすると、
（方法１）　
　Ａ　　＋Ｂ＋Ｃ＋Ｄ　　　＝８１６　・・・　（１）
（方法２）　
　Ａ×３＋Ｂ＋Ｃ＋Ｄ×３＝１３６８　・・・　（２）

（２）−（１）より、
　（Ａ＋Ｄ）×２＝５５２
よって、　Ａ＋Ｄ＝２７６通りとなります。

解答例３

小西孝一さん、 ヌオの母さん、MITUYAMIさん、他

解答例２のパターンＢ、Ｃの場合の数を求めることにします。

さて、各人が自分の顔見知りから１人および顔見知りでない人から１人の合計２人を選ぶ選び方を考えます。（方法 ３）

参考図４

方法３では、ある特定の人から見て、

  • 自分の顔見知りから１人を選ぶ方法：　　12C1＝１２通り

  • 自分の顔見知りでない１人を選ぶ方法：　5C1＝５通り

 合計１２×５＝６０通り、従って全員では、６０×１８＝１０８０通りとなります。

ここで、方法１の選び方４パターンと方法３の選び方との関連を考えます。

１８人の中から任意の３人を選び、ａ、ｂ、ｃとします。
顔見知りと顔見知りでない人の両方を選んでいるので、パターンＢかパターンＣのいずれかになります。

  • パターンＢのとき　・・・　ｂがａ、ｃと顔見知りとします　
    方法３では、aが、顔見知りのｂと顔見知りでないｃを選ぶとき、および
    ｃ    が、顔見知りのｂと顔見知りでないａを選ぶときの２回同じ組み合わせを数えることになる。
    　参考図４−１
    　

  • パターンＣのとき　・・・　ａとｂが顔見知りとします　
    方法３では、ａが、顔見知りのｂと顔見知りでないｃを選ぶとき、および
    ｂ    が、顔見知りのａと顔見知りでないｃを選ぶときの２回同じ組み合わせを数えることになる。
    　参考図４−２

従って、
（方法１）　
　Ａ＋Ｂ＋Ｃ＋Ｄ＝８１６　・・・　（１）
（方法３）　
　Ｂ×２＋Ｃ×２＝１０８０　・・・　（３）

（２）より、
　Ｂ＋Ｃ＝１０８０÷２＝５４０　・・・　（３）'
よって、（１）−（３）'より、
　Ａ＋Ｄ＝８１６−５４０＝２７６通りとなります。