第３０４問の解答

問題　［場合の数］

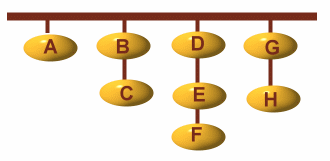問題図 左図は、パン食い競争用にヒモに吊るされたパンをあらわしています。

この競争の参加者（８人）は、かけっこの途中でこのパンを１個、口で取ってゴールに向かわねばなりません。

パンを取るときのルールとして、ヒモの一番下にあるパンを取らなければならないことになっています。（例えば、Ｃのパンよりも先にＢのパンを取ることはできません。）

このとき、パンの取られ方の順番は何通り考えられるでしょうか。

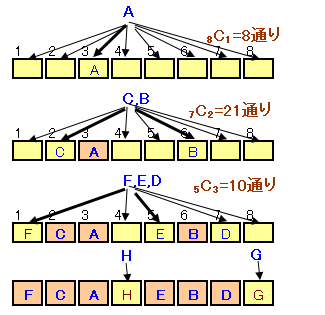
解答例１[組合せ]

Taroさん 、ＡЯＯＴさん、 トトロ＠Ｎさん、ふじさきたつみさん、小西孝一さん、清川育男さん、takamatsuさん、 他

パンを取る順番を１から８までの番号をつけます。

参考図１

同じじひもにぶら下がっているパンの番号を選ぶと、これらのパンのとる順番は一意的に決まります。

  • Ａのパンにつける番号　・・・　8C1＝８通り

  • Ｂ、Ｃのパンにつける番号　・・・　7C2＝２１通り

  • Ｄ、Ｅ、Ｆのパンにつける番号　・・・　5C3＝１０通り

  • Ｇ、Ｈのパンには、残った番号が自動的に決まる

従って、合計８×２１×１０＝１６８０通りとなります。

答：１６８０通り

以上

解答例２［重複組合せ］

あんみつさん 、暇な人間さん 、長野美光さん 、CRYING DOLPHINさん 、他

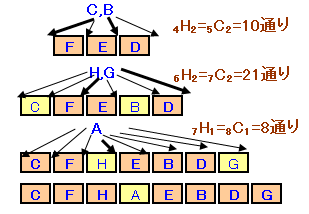
まず、D、E、Fのパンをとる順番をF、E、Dとします。

参考図２

次に、B、Cのパンをとる順番を決めます。
F、E、Dのパンの間および両端の４カ所から重複を許して２個選べばいいので、
　4H2＝4+2-1C2＝１０通り

これで５個のパンの順番がきまったので、これらの間と両端の６カ所から２個選んでG、Hのパンを順番を決めます。
　6H2＝6+2-1C2＝２１通り

最後に、Aの順番を決めます。７個のパンの間よ両端の８カ所から１カ所選べば良いので、
　8H1＝8+1-1C1＝８通り

従って、合計１０×２１×８＝１６８０通りとなります。

（参考）重複組み合わせの解説　

解答例３［順列］

ミミズクはくず耳さん、 ＩＣさん、maruhagedonさん、クララさん、sugitakukunさん、きょえぴさん、中村明海さん、ステップばいステップさん、あまれっとさん、chyusonさん、BossF他

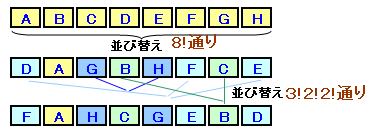
８個のパンを並べ替えます。

参考図３

８個のものから８個選んで並べる順列なので、8P8＝８!通りになります。

これらの中で、同じひもにぶら下がっているパンはとる順番が一通りに決まってしまうので、
　B、Cの並べ替え　　　・・・　2P2＝２!通り
　D、E、Fの並べ替え　・・・　3P3＝３!通り
　G、Hの並べ替え　　　・・・　2P2＝２!通り
を重複して数えていることになります。

従って、求める場合の数は、
　８!／（２!３!２!）＝１６８０通りとなります。

（その他の解法）

  • 樹形図をもちいて場合分け　・・・　M.Hossieさん、ねこやんさん、ラララさん　

    　
  • 漸化式をもちいる　・・・　有無相生さん