第３０５問の解答

問題　［平面図形］

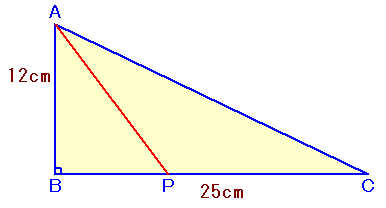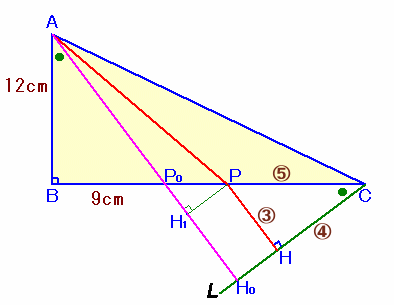
問題図  左図のような、ＡＢ＝１２cm、ＢＣ＝２５cm、∠Ｂ＝９０度の直角三角形ＡＢＣがあります。

この三角形の辺ＢＣ上に点Ｐをとって、「ＡＰの長さ×５＋ＰＣの長さ×３」が最も小さくなるようにします。

では、このときの「ＡＰの長さ×５＋ＰＣの長さ×３」を求めて下さい。

解答例１[算数]

マサルさん、ラララさん、Banyanyanさん、中村明海さん、ステップばいステップさん、 ミミズクはくず耳さん 、永井暁さん、おかひで博士さん、sugitakukunさん、あんみつさん、ねこやんさん、Nの悲劇さん、萬田銀次郎さん、あまれっとさん、まっつぁんさん、他

ｄ＝AP＋PC×３/５とおき、ｄの最小値を下図で求めます。
Lは頂点Cを通り傾きが3/4の直線です。

参考図１

PがBC上にあるとき、Pから直線Lに下ろした垂線の足をHとすると、
PH＝PC×３/５ですから、ｄ＝AP＋PHとなります。

従って、ｄが最小になるのは、A、P、Hが一直線上に並ぶときです。

実際、頂点Aから直線Lに下ろした垂線の足をH0とし、
AH0と辺BCの交点をP0とすると、
PH＝H1H0、AP≧AH1よりAP＋PH≧AH1＋H1H0＝AH0となります。

このとき、△P0ABと△P0CH0は相似より、
　AP0＝AB×５/４＝１２×５/４＝１５cm、
　BP0＝AB×３/４＝１２×３/４＝　９cm、
　P0C＝BC−BP0＝１６ｃｍ。

よって、求める最小値は、
　５AP0＋３P0C＝５×１５＋３×１６＝７５＋４８＝１２３cm　となります。

答：１２３ｃｍ

以上

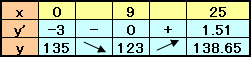
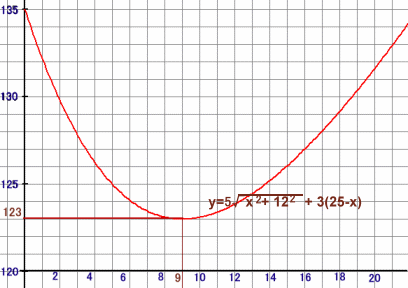
解答例２[微分]

哲也さん、mhayashiさん、武田浩紀さん 、Taroさん 、sodoさん 、辻。さん 、Nagahiroさん 、ばち丸さん 、CRYING DOLPHINさん 、小西孝一さん 、Parpunteさん 、M.Hossieさん 、他

ｘ＝BP、ｙ＝５AP＋３PCとします。
AP＝√（ｘ2＋１２2）、PC＝（２５−ｘ）より、
ｙ＝５√（ｘ2＋１２2）＋３（２５−ｘ）　となります。

ｙの増減を調べるために、ｙを微分して、
ｙ'＝５ｘ／√（ｘ2＋１２2）−３
　＝（５ｘ−３√（ｘ2＋１２2））／√（ｘ2＋１２2）

ｙ'＝0となるのは、
 ５ｘ＝３√（ｘ2＋１２2）
　２５ｘ2＝９ｘ2＋９×９×１６
　１６ｘ2＝９2×１６
よって、ｘ＝９のときです。

従って、ｙの増減表は下表の通り。

参考図２

なお、ｙ＝５√（ｘ2＋１２2）＋３（２５−ｘ）　のグラフは下図のようになります。

参考図３


よって、求める最小値は、１２３cmとなります。

（その他の解法）

  • 座標で解く　・・・　有無相生さん
    双曲線t*t-u*u=12*12（0<u<25)への接線の傾きが5/3になる接点の座標を求める問題に帰着　
    　
  • EXCEL等で計算　・・・　ふじさきたつみさん、ちば けいすけさん