第３０６問の解答

問題　［平面図形 、整数の性質］

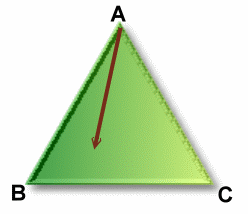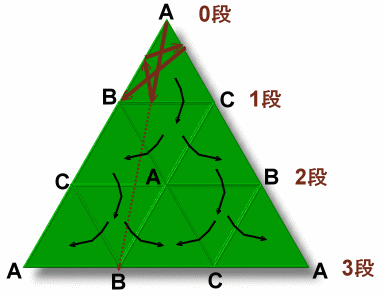
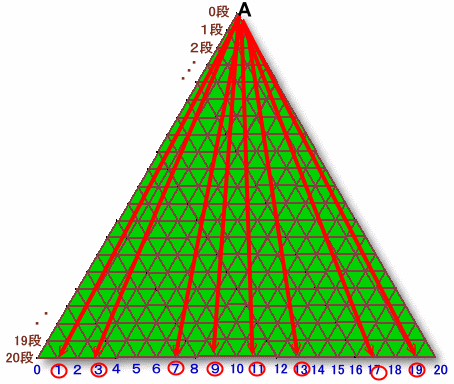
問題図  左図のような正三角形の形をしたビリヤード台があります。
このビリヤード台の各頂点Ａ、Ｂ、Ｃにはポケットと呼ばれる穴があって、そこにやってきたボールは穴に落ちてしまいます。

いま、Ａポケットの位置からボールを打ち出しました。
ボールは各辺にぶつかるとはね返り、どこかのポケットに入るまでこれを続けます。

では、３７回はね返ってポケットに入るような打ち出し方（打ち出し方向）は何通りあるでしょうか。

解答例１[算数]

Taroさん、長野美光さん、ＩＣさん、CRYING DOLPHINさん、Banyanyanさん、 MITUYAMIさん 、Nの悲劇さん、小西孝一さん、中村明海さん、ちば けいすけさん、kokoさん、有無相生さん、M.Hossieさん、BossFさん、他

ボールが跳ね返ってどう進むかは、正三角形のビリヤード台を折り返して考えることができます。

参考図１

上図で、３段目にある４つの頂点のうち、両端を除いたＢ、Ｃの２カ所と最初の頂点Ａを結べば、
ボールは３回跳ね返ってポケットに入ることになります。

一般に、ｎ段目のポケットに入るときには、図の水平な辺に（n-1）回、斜めの辺に（n-2）回交わるので、
合計(2n-3)回跳ね返ります。

従って、ボールが３７回跳ね返ってポケットに入るのは、
　2n-3＝３７
よって、n＝２０段になるときです。

下図は、２０段までビリヤード台を折り返したところを表したところです。

参考図２


２０段目には、両端を除くと１９個の頂点がありますが、これらに向かってボールを打ちだしたとき、
途中でポケットに入ってしまうケースを除く必要があります。

このため、一般的にｎ段目の左からｋ番目の頂点をＴｎ、ｋと表すことにします。
Ｔ0、0からＴｎ、ｋへ打ち出したときに、途中でポケット（Ｔm、ｊ）に入るとしたら、
　n＝pm、k=pjとなるpが存在するとき、すなわちｎとｋが公約数を持つときになります。

従って、２０段目のＴ20、ｋのポケットにちょうど入るには、ｋが２０と互いに素である必要があります。

１から１９までの整数で２０と互いに素となるのは、
　１、３、７、９、１１、１３、１７、１９
の８通りです。

答：　８通り

以上