第３０７問の解答

問題　［平面図形 ］

問題図
上の図のような二等辺三角形Ａ、Ｂがそれぞれたくさんあります。

いま、この２種類の三角形を何枚か使い、隙間がないように並べて三角形を作ります。
例えば、Ａの三角形とＢの三角形を１枚ずつ使った場合は、上の図の右のような三角形が出来ますね。

このとき、使う三角形の枚数（ＡとＢの合計）として考えられるもののうち、２ケタでかつ素数であるものをすべて答えて下さい。

解答例１[算数]

ステップ　ばい　ステップさん、Toru Fukatsuさん、有無相生さん

問題の三角形は図１のように、正五角形を分割してつくることができます。

参考図１

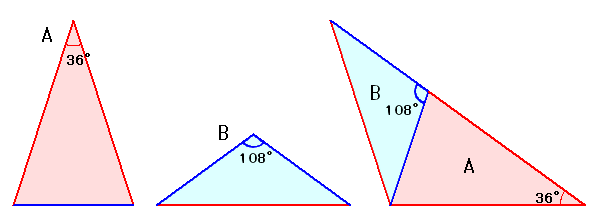
(補題１)Ａ、Ｂの２つの辺a、ｂの比、面積比は、（１＋√５）／２・・・無理数

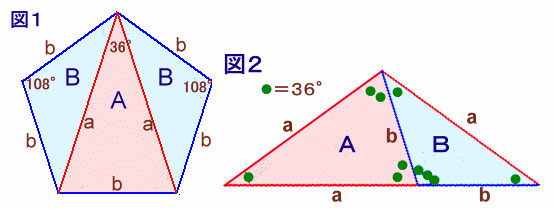
三角形Ａの斜辺の長さをa、底辺の長さをbとし、辺の比a/ｂ（=ｘとおきます）を求めてみます。

図２より、Ａ＋Ｂの三角形はＢと相似、
よって、(a＋b)：a＝a：b。
　　1＋b/a＝a/b
　　1＋1/x＝x
　　x2−ｘ−１＝０
この２次方程式の正の根より、ｘ＝（１＋√５）／２と求まるので、辺の比a/ｂは無理数となります。

次に、三角形ＡとＢの面積比を求めます。

図２より、
　　x2・Ｂ＝Ａ＋Ｂ
よって、
　Ａ／Ｂ＝x2−１＝ｘ＝（１＋√５）／２となり、これも無理数となります。

(補題２)題意のような三角形（合成三角形と呼びます）はＡまたはＢと相似なものに限る

合成三角形は、ＡまたはＢと相似なものに限ることが次のようにして分かります。

合成三角形はＡ、Ｂを敷き詰めて作るので、３つの頂点の角度は、ＡまたはＢの頂点の角度、あるいはこれらの和になります。
ところが、Ａ、Ｂの頂点の角度は、いずれも３６度の倍数なので、合成三角形の頂点の角度も、３６度の倍数となります。

これらを小さい順にk1×３６度、k2×３６度、k3×３６度、とおくと、
　k1×３６度＋k2×３６度＋k3×３６度＝１８０度
従って、k1＋k2＋k3＝５となります。

この条件を満たすのは、k1＝１、k2＝１、k3＝３（三角形Ｂ）またはk1＝１、k2＝２、k3＝２（三角形Ａ）しかありません。

(補題３）合成三角形は敷き詰めるＡ、Ｂの個数は一意的に決まる

ある合成三角形をＡ、Ｂで敷き詰めるたとき、Ａ、Ｂの個数の組み合わせ方が２通りあったと仮定します。
すると、この合成三角形の面積が、２組の整数ｐ、ｑとｐ'、ｑ'により、
　ｐＡ＋ｑＢ＝ｐ'Ａ＋ｑ'Ｂと表されることになります。

これより、（ｐ−ｐ'）Ａ＝（ｑ'−ｑ）Ｂ、
よって、Ａ／Ｂ＝（ｑ'−ｑ）／（ｐ−ｐ'）となり、Ａ／Ｂが無理数であることに反します。

従って、Ａ、Ｂの個数は一意的に決まります。
　

また、合成三角形の各辺の長さは、Ａ、Ｂの辺の長さの和となりますが、いずれか一辺の長さが決まれば残りの二辺も決まります。

そこで、合成三角形、およびこれを敷き詰めるＡ、Ｂの個数合計を、次のように名付けることとします。
（ただし、ｍ≧０、ｎ≧０で、ｍ、ｎいづれかは０でない整数）

  • Ａと相似で、底辺の長さがma＋nbと表せる合成三角形　・・・　Ａ（ｍ、ｎ）
    これらを敷き詰めるＡ、Ｂの個数合計　　　　　　　　　　　・・・　Ｐ（ｍ、ｎ）
    　

  • Ｂと相似で、斜辺の長さがma＋nbと表せる合成三角形　・・・　Ｂ（ｍ、ｎ）　
    これらを敷き詰めるＡ、Ｂの個数合計　　　　　　　　　　　・・・　Ｑ（ｍ、ｎ）

残るは、Ａ（ｍ、ｎ）、Ｂ（ｍ、ｎ）をどう敷き詰めるかだけになります。

(補題４）Ｐ（ｍ、ｎ）＝（３ｍ＋ｎ）（ｍ＋ｎ）、Ｑ（ｍ、ｎ）＝（ｍ＋ｎ）2＋ ｍ2

まず、Ａ（ｍ、ｎ）について考えます。

参考図２

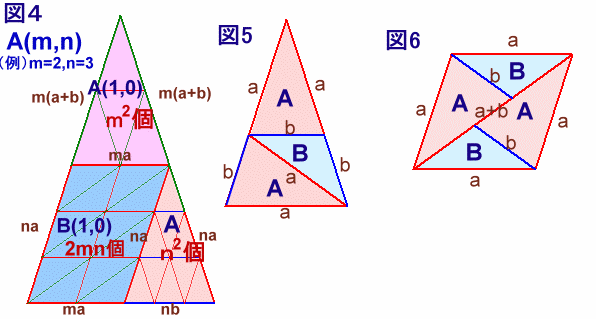
図４のように、Ａ（ｍ、ｎ）は、

  • Ａ（０，１）＝A　・・・　ｎ2個

  • Aと相似で底辺の長さがaのもの＝A（１，０）　・・・　ｍ2個

  • Bと相似で斜辺の長さがaのもの＝B（１，０）　・・・　２ｍｎ個

に分割できます。

また、図５、６より、A（１，０）＝２A＋B、およびB(１，０）＝A＋B　と分かるので、
　Ａ（ｍ、ｎ）
＝ｎ2A＋ｍ2（２A＋B）＋２ｍｎ（A＋B）
＝（２ｍ2＋２ｍｎ＋ｎ2）A＋（ｍ2＋２ｍｎ）B

よって、P（ｍ、ｎ）
＝（２ｍ2＋２ｍｎ＋ｎ2）＋（ｍ2＋２ｍｎ）
＝３ｍ2＋４ｍｎ＋ｎ2
＝（３ｍ＋ｎ）（ｍ＋ｎ）

　

次に、Ｂ（ｍ、ｎ）について考えます。

参考図３

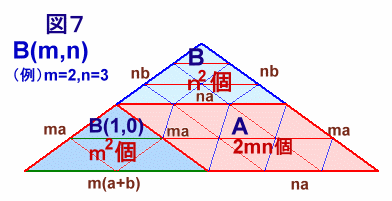
図５のように、Ｂ（ｍ、ｎ）は、

  • Ｂ（０，１）＝Ｂ　・・・　ｎ2個

  • Bと相似で斜辺の長さがaのもの＝B（１，０）・・・　ｍ2個

  • Ａ（０，１）＝Ａ　　・・・　２ｍｎ個

に分割できます。

従って、Ｂ（ｍ、ｎ）
＝ｎ2Ｂ＋ｍ2（A＋B）＋２ｍｎA
＝（ｍ2＋２ｍｎ＋ｎ2）A＋ｍ2B

よって、Ｑ（ｍ、ｎ）
＝（ｍ2＋２ｍｎ＋ｎ2）＋ｍ2
＝（ｍ＋ｎ）2＋ｍ2

　

補題４より、P（ｍ、ｎ）＝（３ｍ＋ｎ）（ｍ＋ｎ）となるが、これが素数となるには、ｍ＋ｎ＝１でなければならない。
このとき、ｍ＝０、ｎ＝１またはｍ＝１、ｎ＝０となり、３ｍ＋ｎ≦３（ｍ＋ｎ）＝３となるので２桁の整数にはならない。

よって、Ａと相似な合成三角形は題意を満たさない。

補題４より、Ｑ（ｍ、ｎ）＝（ｍ＋ｎ）2＋ｍ2となり、これが２桁以下の整数となるものは下表のとおり。

参考図４

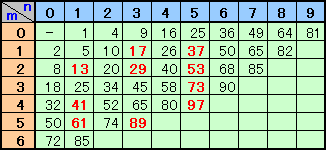
題意を満たす２桁の素数となるのは、
　１３、１７、２９、３７、４１、５３、６１、７３、８９、９７
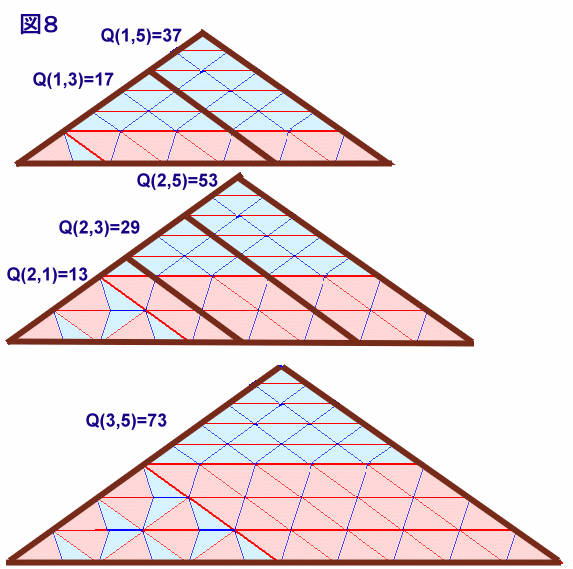
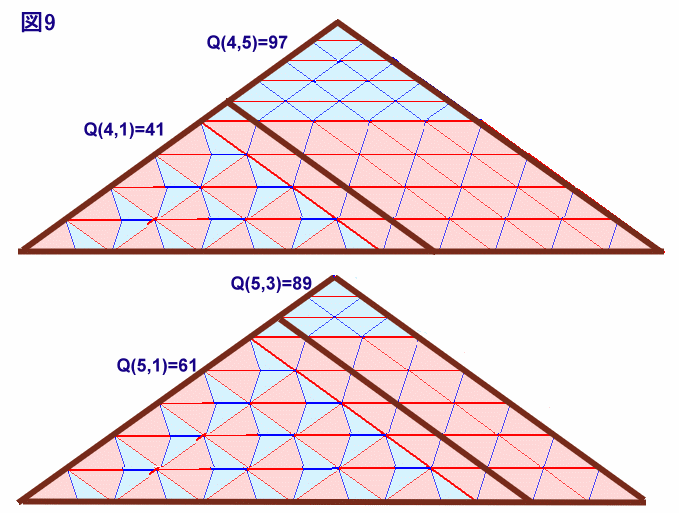
の１０通りとなります。（図８、図９参照）

参考図５

参考図６

答：　１３、１７、２９、３７、４１、５３、６１、７３、８９、９７

以上