第３０９問の解答

問題　［空間図形］

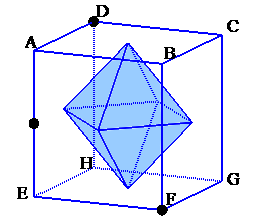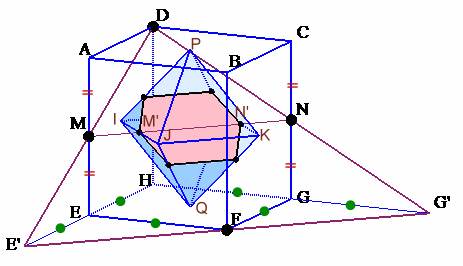
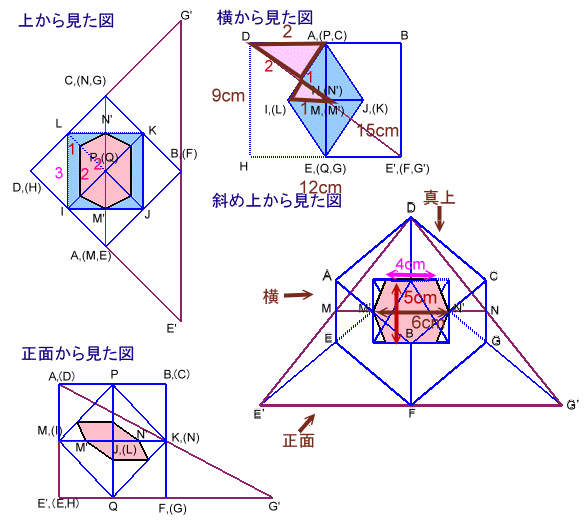
問題図  左図のような直方体ＡＢＣＤ−ＥＦＧＨがあります。この直方体は、四角形ＡＢＣＤ、ＥＦＧＨが面積７２cm2の正方形で、ＡＥ＝ＢＦ＝ＣＧ＝ＤＨ＝９cmとなっています。

いま、図のように各面の中心（対角線の交点）をむすんで八面体を作りました。

この直方体を図の３つの点（ 点Ｄ、点Ｆおよび辺ＡＥの中点）を通る平面で切断します。このとき、図の八面体の切断面の面積は何cm2でしょうか。

解答例１

まるケンさん、ミミズクはくず耳さん、トトロ＠Ｎさん 、小杉原　啓さん、あんみつさん、うっしーさん、ねこやんさん、小西孝一さん、中村明海さん、ちば けいすけさん、有無相生さん、ひめぞうさん、あさみかずみさん、他　多数

八面体の各頂点およびAEの中点に下記のような名前を付けます。
また、切断面とHEの交点をE'、HGとの交点をG'、CGとの交点をMとします。

参考図１

△DE'Hと△ME'Eは相似でDH：ME'＝２：１より、E'H：E'E＝２：１、
よって、E'E＝EHとなります。

すると、△E'HG'と△E'EFが相似でE'H：E'E＝２：１より、HG'：HG＝２：１、
よって、GG'＝GHとなります。

従って、△G'DHと△G'NGの相似より、NがCGの中点となります。

以上より、各図形は平面DHFBに関して左右対称となっていることが分かります。

参考図２

そこで、上図のように図形を各方向から眺めてみると、
八面体の切断面は台形を２つ合わせたような六角形となることが分かります。

この六角形の頂点で、台形の底面となる辺の両端にあたる点をＭ'、Ｎ'とすると、
M'、N'は平面IJKL上にあり、対称性からM'はIJの中点、N'はKLの中点となります。

従って、Ｍ'Ｎ'の長さは正方形ＩＪＫＬの１辺の長さと等しくなります。
正方形ＩＪＫＬの面積＝正方形ＡＢＣＤの面積×１/２＝７２×１/２＝３６。
よって、Ｍ'Ｎ'＝６ｃｍと求まります。

次に、直角三角形△ＤＨＦについて、ＤＨ＝９ｃｍ、ＨＦ＝ＩＪ×２＝１２ｃｍより、
辺の長さが３：４：５の直角三角形となることが分かります。
従って、ＤＦ＝１５ｃｍとなります。

横から見た図で三角形の相似より、
　六角形の高さ＝ＤＦ×１/３＝１５ｃｍ×１/３＝５ｃｍ。

また、上から見た図で三角形の相似より、
台形の上の辺の長さ＝ＬＩ×２/３＝６ｃｍ×２/３＝４ｃｍ。

よって、
　切断面である六角形の面積＝1/2×（６＋４）×（５×1/2）×２＝２５ｃｍ2となります。
　

答：　２５ｃｍ2

以上

（参考）動く３Ｄ図

（その他の解法）