第３１１問の解答

---

問題　［平面図形］

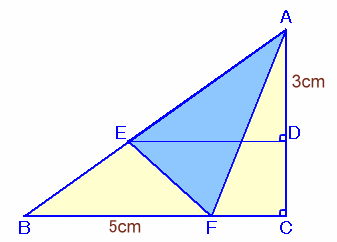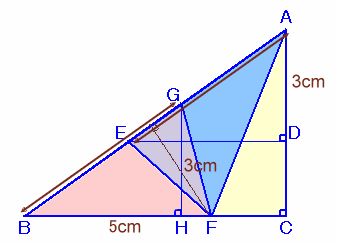
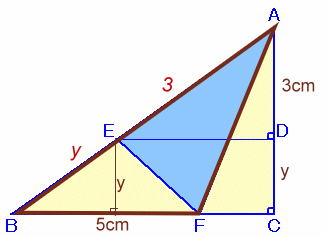
		左図のような∠Ｃ＝９０度の直角三角形ＡＢＣがあり、 点Ｄは辺ＡＣ上の点で、ＡＤ＝３cm、 点Ｆは辺ＢＣ上の点でＢＦ＝５cm 点Ｅは辺ＡＢ上の点で、ＥＤと辺ＢＣは平行 になっています。 このとき、△ＡＥＦの面積を求めて下さい。

---

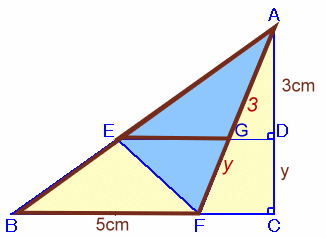
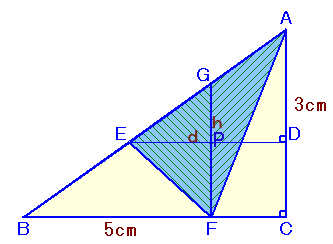
解答例１

長野　美光さん、他

	点Ｇを辺ＡＢ上にＢＧ＝ＥＡとなるようにとり、点Ｇから辺ＢＣに下ろした垂線の足をＨとします。 △ＡＥＦと△ＧＢＦは、底辺ＡＥ＝底辺ＢＧで高さが共通なので、面積は等しい。 また、△ＡＥＤと△ＧＢＨは相似な直角三角形でしかも斜辺の長さが等しいので合同。 よって、ＧＨ＝ＡＤ＝３ｃｍ。 従って、△ＡＥＦ＝△ＧＢＦ＝1/2×ＢＦ×ＧＨ＝1/2×５×３＝７．５cm2。 　 答：　７．５cm2 以上

---

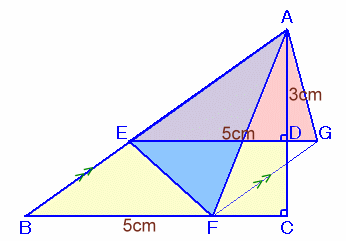
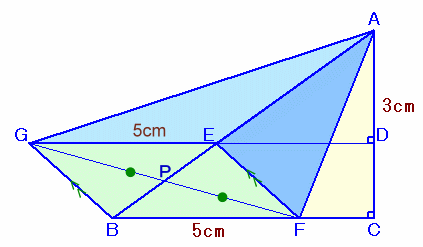
解答例２

真島　嘉弘TZさん、Nonさん、きよたんさん、大岡　敏幸さん、他

	Fを通りＢＡに平行な直線とＥＤの延長線との交点をＧとします。 ＥＢＦＧは平行四辺形となるので、ＥＧ＝ＢＦ＝５ｃｍ。 また、ＢＡとＦＧが平行より、 　△ＡＥＦ＝△ＡＥＧ＝1/2×ＥＧ×ＡＤ＝1/2×５×３＝７．５cm2。

---

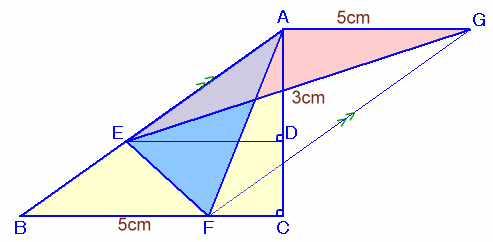
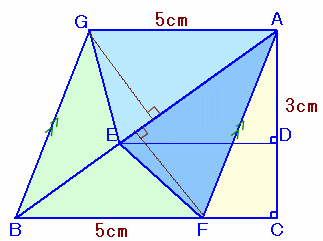
解答例３

CRYING DOLPHINさん、他

	Fを通りＢＡに平行な直線とＡを通りＢＣに平行な直線との交点をＧとします。 ＥＢＦＧは平行四辺形となるので、ＡＧ＝ＢＦ＝５ｃｍ。 また、ＢＡとＦＧが平行より、 　△ＡＥＦ＝△ＡＥＧ＝1/2×ＡＧ×ＡＤ＝1/2×５×３＝７．５cm2。

---

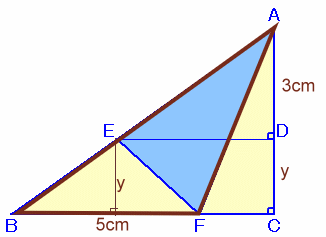
解答例４

Banyanyanさん、まるケンさん、有無相生さん、nobさん、ばち丸さん、他

	ＤＧ＝ｙとします。 　△ＡＥＦ ＝△ＡＢＦ−△ＥＢＦ ＝1/2×ＢＦ×ＡＤ−1/2×ＢＦ×ＤＣ ＝1/2×５×（３＋ｙ）−1/2×５×ｙ ＝1/2×５×３ ＝７．５cm2。

---

解答例５

ミミズクはくず耳さん、さと先さん、トトロ＠Ｎさん、ひめぞうさん、他

	ＥＤとＢＣが平行より、ＡＥ：ＥＢ＝ＡＤ：ＤＣ＝３：ｙ。 　△ＡＥＦ ＝△ＡＢＦ×３／（ｙ＋３） ＝1/2×ＢＦ×ＡＣ×３／（ｙ＋３） ＝1/2×５×（３＋ｙ）×３／（ｙ＋３） ＝1/2×５×３ ＝７．５cm2。

---

解答例６

ＩＣさん、ちば けいすけさん、dottoreさん、他

	ＥＤとＡＦの交点をＧとします。 ＥＤとＢＣが平行より、ＡＧ：ＧＦ＝ＡＤ：ＤＣ＝３：ｙ。 よって、ＥＧ＝ＢＦ×３／（３＋ｙ）＝１５／（３＋ｙ）。 　△ＡＥＦ ＝△ＡＥＧ×（３＋ｙ）／３ ＝1/2×ＥＧ×ＡＤ×（３＋ｙ）／３ ＝1/2×１５／（３＋ｙ）×３×（３＋ｙ）／３ ＝1/2×１５ ＝７．５cm2。

---

解答例７

ねこやんさん、他

	Ｂを通りＦＥに平行な直線とＤＥの延長線との交点をＧとします。 ＧＢＦＥは平行四辺形だから、ＧＥ＝ＢＦ＝５ｃｍ。 また、平行四辺形ＧＦＢＥの対角線の交点をＰとすると、ＧＰ＝ＰＦ。 よって、△ＡＧＰ＝△ＡＰＦ、△ＥＧＰ＝△ＥＰＦ、 従って、△ＡＧＥ＝△ＡＧＰ−△ＥＧＰ＝△ＡＰＦ−△ＥＰＦ＝△ＡＥＦ。 よって、△ＡＥＦ＝△ＡＧＥ＝1/2×ＧＥ×ＡＤ＝＝1/2×５×３＝７．５cm2。

---

解答例８

ふじさきたつみさん、他

	Ａを通りＣＢと平行な直線と、Ｂを通りＦＡと平行な直線の交点をＧとします。 ＧＢＦＡは平行四辺形となるから、ＧＡ＝ＢＦ＝５ｃｍ、 △ＧＢＡと△ＦＡＢは合同。 よって、△ＡＥＦと△ＡＥＧは、底辺ＡＥが共通で高さが等しいので、面積も等しい。 △ＡＥＦ＝△ＡＥＧ＝1/2×ＧＡ×ＡＤ＝1/2×５×３＝７．５cm2。

---

解答例９

川田智之さん、他

	Ｆを通りＣＡと平行な直線と、ＡＢとの交点をＧとし、ＥＤとＧＦの交点をＰとします。 ＧＦ＝ｈ、ＥＤ＝ｄとおくと、 △ＡＥＤと△ＧＢＦが相似より、ＡＤ：ＥＤ＝ＧＦ：ＢＦ、３：ｄ＝ｈ：５。 よって、ｄ×ｈ＝３×５＝１５。 　△ＡＥＦ ＝△ＧＥＦ＋△ＡＧＦ ＝1/2×ＧＦ×ＥＰ＋1/2×ＧＦ×ＰＤ ＝1/2×ＧＦ×（ＥＰ＋ＰＤ） ＝1/2×ｈ×ｄ ＝1/2×５×３ ＝７．５cm2。

---

（その他の解法）

• 特殊な場合（Ｄ＝Ｆ＝Ｃ）で考える　・・・　ＡЯＯＴさん、中村明海さん、kokoさん、あさみかずみさん、 他
  　
• 特殊な場合（直角二等辺三角形）で考える　・・・　航介さん、 他
  　
• 特殊な場合（辺の長さが３：４：５の直角三角形）で考える　・・・　小西孝一さん、あんみつさん、他
  　
• 長方形にして等積変形　・・・　TONOさん、