第３１２問の解答

問題　［確からしさ］

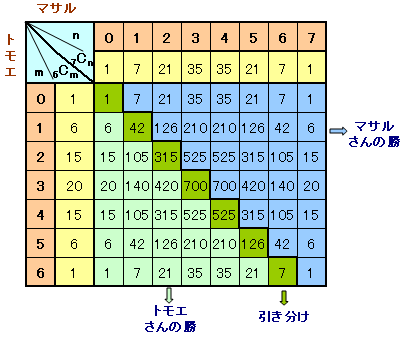
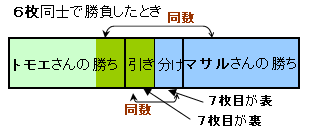
マサルさんとトモエさんが「コイン投げゲーム」をしています。

そのルールは、
　「２人がそれぞれ６枚のコインを投げ、表の出た枚数が多いほうが勝ち（注）」、
というものでした。

ところが、どうしても勝ちたいマサルさんは、インチキをして７枚のコインを投げたそうです。
このとき、マサルさんが勝つ確からしさ（確率）を求めて下さい。

（注）表の枚数が同じ場合は、「引き分け」でゲームは終了です。 　

解答例１

長野　美光さん、Taroさん、トトロ＠Ｎさん、ミミズクはくず耳さん、あんみつさん、うっしーさん、真島　嘉弘TZさん、ＩＣさん、CRYING DOLPHINさん、モルモット大臣さん、うききさん、まるケンさん、ハラギャーテイさん、有無相生さん、u-tyanさん、Miki Sugimotoさん、　ねこやんさん、永井　暁さん、他

マサルさんが投げた７枚のコインのうちn枚表となる場合は7Cn、
トモエさんが投げた６枚のコインのうちm枚表となる場合は6Cmとなります。

参考図１

従って、マサルさんが勝つ場合の数は、m<nとなる場合の6Cm×7Cnの和となります。
これは、上図の青色の部分に相当します。

ところが、２項定理の対称性(pCq=pCp-q)より、青色部分と残りの部分（うす緑、濃い緑の部分）は、ちょうど同じ数が対称的に並んでいるので、場合の数は等しくなります。

よって、マサルさんが勝つ確率は１/２となります。

答：　１/２

以上

解答例２

chiocciolaさん、拓パパさん、中村明海さん、まるケンさん、M.Hossieさん、ふじさきたつみさん、清川　育男さん、nob-kishさん、岡野ＰＲＴさん、大岡　敏幸さん、他

まず、マサルさんの７枚目を除く６枚同士でトモエさんと勝負を考えてみます。

参考図２

同じ枚数ですから、勝ちと負けの場合の数は等しくなります。

ズルをした場合のマサルさんの勝ちとなるケースは、
　６枚同士で既に勝ちとなるケース　・・・　（１）
　６枚同士では引き分けで、残る一枚が表となるケース　・・・　（２）
の２通りあります。

このうち、
　（１）は、６枚同士でトモエさんの勝ちのケースと同数、
　（２）は、６枚同士では引き分けで、残る一枚が裏となるケースと同数
なので、最終的には、
　マサルさんの勝ちのケースの数＝引き分けか負けるケースの数
となり、勝つ確率は１/２となります。

（その他の解法）